Semigroups and Groups
DiscreteÇÑ ±¸Á¶¸¦ ÀÌÇØÇϱâ À§ÇÏ¿© ÇÊ¿äÇÑ ¿©·¯
¼öÇÐ ÀÌ·Ð Áß¿¡¼ ¸ÕÀú ±âº»ÀûÀÎ semigroup °ú
groupÀÇ °³³äÀ» ¾Ë¾Æº¸°í computer À̷п¡
È°¿ëÇÏ´Â ¹æ¹ý¿¡ °üÇÏ¿© ÇнÀÇϵµ·Ï ÇսôÙ.
´ÙÀ½ÀÇ °ÀÇ ³»¿ëÀº B. Kolman, R.C. Bussy & S.
RossÀÇ Àú¼ÀÎ
Discrete Mathematical Structures,
Prentice Hall Inc., 1996.
ÀÇ 9ÀåÀÇ ³»¿ëÀ» Âü°íÇÏ¿© ÇнÀÇϱ⠹ٶø´Ï´Ù.
(1) Binary Operations Revisited
¡ß A binary operation on a set A is an
everywhere defined function f : A x A¡æA
- f is defined for each ordered pain of (a,b)
- only one element of A is assigned to each
(a,b)
- if a,b¡ôA then a*b¡ôA ; A is closed under the
operation *
¡ß Properties of binary operations.
- a binary operation * on a set A is said to be
commutative if a*b = b * a for all a,b¡ôA
- a binary operation * on a set A is said to be
associative if
a*(b*c)= (a*b)*c for all a,b,c¡ôA
- a binary operation * on a set is said to be
idempotent if a*a = a for all a¡ôA
(2) Semigroups
¡ß A Semigroups is a nonempty set S together
with an associative binary operation * defined
on S.
- we refer to a*b as the product of a and b.
- the semigroup (S,*) is said to be commutative if
* is a commutative operation.
- let A = (a1, a2, ... , an) be a nonempty set, then
(A*,, (concatenation)) is a semigroup since
(¥á,¥â),¥ã = ¥á,(¥â,¥ã) for ¥á,¥â,¥ã¡ôA* .
The semigroup (A*, , ) is called the free
semigroup generated by A
¡ß An element e in a semigroup (S,*) is called
an identity if e*a=a*e=a for all a¡ôS
(Example) The number 0 is an identity in the
semigroup (Z,+)
The semigroup (Z+,+) has no identity element.
- If a semigroup (S,*) has an identity, it is unique.
[Suppose that e and e' are identity elements in S,
then e*e'=e' and e*e'=e', hence e = e'.]
¡ßA monoid is a semigroup (S,*) that has an
identity.
¡ß Let (S,*) be a semigroup and T¡øS
- If T is closed under the operation *, then
(T,*) is a subsemigroup of (S,*).
- If e (identity)¡ôT, then (T,*) is a submonoid
of (S,*).
¡ß Let (S,*) and (T,*') be two semigroups.
- a function f:S¡æT is called an isomorphism
from (S,*) to (T,*') if it is one to one
correspondence and f(a*b)=f(a)*'f(b) for
every a, b in S.
-f is an isomorphism from S to T, then
f-1 is an isomorphism from T to S.
Example. Let T be the set of all even
integers, then ( Z ,+) and ( Z ,+) are
isomorphic define f : Z ¡æT by f(a) = 2a,
thenf is one-to-one and onto (hence
one-to-one correspondence) and f(a+b) =
2(a+b) = 2a + 2b = f(a) + f(b) . |
Theorem 2. Let (S,*) and ( T,*') be
monoids with respective identities e and
e'. Let f : S¡æT be an isomorphism, then
f(e)=e'.
|
Proof. Let a¡ô S and b¡ô T and f(a) = b
b = f(a) = f(e*a) = f(a)*'f(e)=b*'f(e), hence
f(e)=e'. Q.E.D.
¡ß Let (S,*) and ( T,*') be two semigroups.
- an everywhere defined function f : S¡æT is
called a homomorphism from (S,*) to ( T,*') if
f(a*b) = f(a)*'f(b) for every a, b in S.
- if f is also onto T is the homomorphic image
of S.
Theorem 4. Let f be a homomorphism from a
semigroup (S,*) to semigroup ( T,*')
If S' is a subsemigroup of (S,*) then f(S'),
the image of S' under f is a subsemigroup of
( T,*').
|
Proof. If t1,t2¡ô f(S') then t1=f(s1) and
t2=f(s2) for some s1,s2 .
t1*' t2 = f (s1 ) *'f (s2 ) = f (s1*s2 ) = f (s3)
where s3¡ô S', hence t1*' t2 = f(S')
Q.E.D.
Theorem 5. If f is a homomorphism from a
commutative semigroup (S,*) onto a
semigroup ( T,*') then ( T,*') is also
commutative .
|
Proof. Let t1,t2¡ô T then t1= f(s1) and
t2=f(s2) for s1,s2¡ôS.
t1*' t2 = f (s1 ) *'f (s2 )
= f (s1*s2 ) = f (s2*s1 ) = f (s2 ) *'f (s1)
= t2 *' t1.
Q.E.D.
(3) Products and Quotients of
Semigroups
Theorem 1. If (S,*) and ( T,*') are
semigroups then ( S x T,*'') is a semigroup,
where *'' is defined by s1,t1*'' s2,t2=(s1*s1 ,
t1*' t2 ).
|
¡ß An equivalence relation R on the semigroup
(S,*) is called a congruence relation if aRa'
and bRb' implies (a*b)R(a'*b' ).
Example. Let A ={0,1} . Consider the semigroup
(A*, . ) :
¥áR¥â iff ¥á and ¥â have the same number of
1's (¥á,¥â¡ôA*)
¥áR¥á for any ¥á¡ôA*, if ¥áR¥â then ¥âR¥á
¥áR¥â and ¥âR¥ã, then ¥áR¥ã. Hence R is an
equivalence relation
¥áR¥á' and ¥âR¥â' then (¥á,¥â)R(¥á',¥â' )
Hence R is a congruence relation.
|
¡ßLet [a] be the equivalence class containing
a, and let S/R be the set of all equivalence
classes.
Theorem 2. Let R be a congruence relation on
the semigrouop (S,*) . Consider the relation
 from S/R x S/R to S/R where ([a],[b]) is from S/R x S/R to S/R where ([a],[b]) is
related to [a*b]. Then we have
(a)  is a function from is a function from
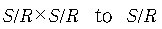 . .
(b) (S/R, ) is a semigroup. ) is a semigroup.
|
Proof. (a) Suppose ([a],[b]) = ([a'],[b']) ,
then and aRa' and bRb' so a*bRa'*b' , thus
([a],[b]) = ([a'],[b']) ; that is,  is a is a
function .
(b) [a]  ([b] ([b]  [c]) = [a] [c]) = [a]  [b*c ] [b*c ]
= [a*(b*c) ] = [(a*b)*c ]
= [a*b]  [c] = ([a] [c] = ([a]  [b]) [b])  [c] [c]
¡ß S/R is called the quotient semigroup or
factor semigroup.
Example. S=(A*, . ) , A = {0, 1},
then (S/R,¢Á ) is a monoid where
[¥á]¢Á[¥â]=[¥á.¥â].
Theorem 3. Let R be a congruence relation on
a semigroup (S,*), and (S/R, ) let be the ) let be the
corresponding quotient semigroup, Then the
function fR:S¡æS/R defined by fR(a)= [a] is
an onto homomorphism .
|
Proof. If [a]¡ôS/R then fR(a)= [a] so fR is
onto. Let a,b¡ôS, then
fR(a*b)= [a*b]=[a] [b]=fR(a) [b]=fR(a) fR(b) fR(b)
¡ß fR : S ¡æ S/R is called
the natural homomorphism.
Theorem 4. Let f : S¡æT be a homomophism of
the semigroup (S,*) onto the semigroup . Let
R be a relation on S defined by aRb iff f(a) =
f(b) a,b¡ôS.
Then (a) R is a congruence relation;
(b) (T,*') and the quotient semigroup
(S/R, ) are isomorphic . ) are isomorphic . |
Proof. (a) It is easy to show that R is an
equivalence relation. Suppose aRa' and bRb'.
Then f(a) = f(a') and f(b) = f(b')
f(a) *'f(b) = f(a') *'f(b')
f(a*b) = f(a'*b') , hence a*bRa' *b'
(b) Define 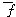 : S/R ¡æT as follows : S/R ¡æT as follows
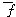 ([a]) = f([a]) for each [a] in S/R. ([a]) = f([a]) for each [a] in S/R.
Suppose [a]=[a'] then aRa' so f(a) = f(a') ,
hence 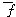 is a function. is a function.
Suppose that 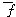 ([a]) = ([a]) = 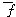 ([a']) then f(a) = ([a']) then f(a) =
f(a'), so aRa' ¢¡ [a]=[a'], hence 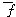 is is
one-to-one.
Suppose b¡ôT, then f(a) = b a¡ôT.
then 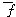 ([a]) = f(a) = b , hence ([a]) = f(a) = b , hence 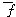 is onto. is onto.
Finally,
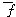 ([a] ([a] [b])= [b])=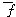 ([a*b]) = f(a*b) =f(a) *'f(b) ([a*b]) = f(a*b) =f(a) *'f(b)
= 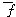 ([a]) *' ([a]) *' 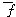 ([a]) ([a])
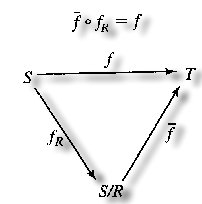
( 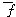 °fR)(a) = °fR)(a) = 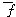 (fR(a)) = (fR(a)) = 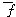 [(a)]= f(a) [(a)]= f(a)
(4) Groups
¡ßA group is a set G together with a binary
operation * on such that
1.(a*b)*c a* (b*c) for a,b,c ¡ôG;
2. there is unique element e in G such that
a*e = e*a = a for a ¡ôG;
3. For every a ¡ôG there is a' ¡ôG
(inverse of a) such that a*a' = a'*a = e.
¡ßA group G is said to be abelian if a*b =
b*a for all a,b ¡ôG.
Theorem 1. Let G be a group. Each
element a ¡ôG has only one inverse in G.
|
Proof. Let a and a' be inverse of a.
Then a'(aa'') = a'e=a'
a'(aa'') =ea'=a'' Hence a'=a''.
Q.E.D.
¡ß We denote the inverse of a by a-1.
Theorem 2. Let G be a group and a,b,c¡ôG .
Then
(a) ab = ac ¢¡ b = c;
(b) ba = ca ¢¡ b = c.
|
Theorem 3. Let G be a group and a,b¡ôG.
Then
(a) (a-1)-1 = a ;
(b) (ab)-1= b -1 a -1.
|
Theorem 4. Let G be a group and a,b¡ôG .
Then
(a) The equation ax = b has a unique
solution in G.
(b) The equation ya = b has a unique
solution in G.
|
Proof. (a) x = a -1b is a solution since a(a -1b)=
(aa-1)b = eb = b.
Suppose x1 and x2 are two solution of ax = b.
Then ax1 = b and ax2 = b Hence ax1 = ax2 ¢¡ x1 =
x2 .
¹®Á¦ 1. À§ Á¤¸® 4ÀÇ (b)¸¦ Áõ¸íÇϽÿÀ.
|
¡ß If a group G is finite, binary operation * can
be given by a table.
- from Theorem 4, each element b must
appear exactly once in each row and column of
the table.
¡ß If G is a group that has a finite number of
elements, we say that G is a finite group and
order of G is |G|.
The following is the multiplication table for
groups of orders 1, 2, 3 .
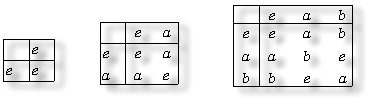
- The groups of orders 1, 2 and 3 are also
abelian and that there is just one group
of each order for a fixed labeling of the
elements .
¡ß Let H be a subset of a group G such that
(a) e¡ôH
(b) if a,b¡ôH then ab¡ôH
(c) if a¡ôH then a-1¡ôH
then H is called a subgroup of G.
Theorem 5. Let (G,*) and (G',*') be two
groups, and let f:G¡æG' be a homomorphism
from G to G'. The we have
(a) If e¡ôG and e'¡ôG' are identities then
f(e)=e'.
(b) If a¡ôG, then f(a-1)=(f(a))-1.
(c) If H is a subgroup of G, then
f(H) ={f(h) | h¡ôH} is a subgroup of G'.
|
Proof. Let x=f(e). Then
x*x'=f(e)*'f(e)=f(e*e)=f(e)=x so x*'x=x
multiply both sides by x-1
x*'x*'x-1 = x*'x-1¢¡x*e'=e'¢¡x=e' so f(e)=e'
f(a-1*a) =f(a-1) *'f(a) =f(e)=e'
Hence f(a-1) =(f(a)) -1.
Q.E.D.
¹®Á¦ 2. À§ Á¤¸® 5ÀÇ (b), (c)¸¦ Áõ¸íÇϽÿÀ.
|
(5) Products and Quotients of
Groups
Theorem 1. If G1 and G2 are groups, then
G=G1xG2 is a group with operation defined
by (a1,b1)(a2,b2) = (a1a2 , b2b1).
|
Theorem 2. Let R be a congruence relation on
the group (G,*). Then the semigroup (G/R, ) )
is a group, where the operation  is defined is defined
on G/R by [a] [a]=[a*b]. [a]=[a*b].
|
Proof. Since a group is a monoid G/R is a
monoid. Let [a]¡ôG/R, then [a-1]¡ôG/R and
[a] [a-1]=[a*a-1]=[e]. [a-1]=[a*a-1]=[e].
So [a]-1=[a-1] hence (G/R, ) is a group. ) is a group.
Q.E.D.
Corollary 1.
(a) If R is a congruence relation on a group ,
then the function fR:G¡æG/R given by fR(a)=
[a] is a group homomorphism.
(b) If f:G¡æG' is a homomophism from the
group (G,*) onto the group (G',*'), and R is
a relation defined on G by aRb iff f(a)=f(b) ,
a,b¡ôG; then we have
(1) R is a congruence relation;
(2) The function 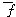 :G/R¡æG' , given by :G/R¡æG' , given by 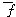
([a])=f(a) is an isomorphism from the group
(G/R, ) onto the group (G',*'). ) onto the group (G',*').
|
|