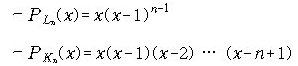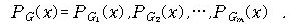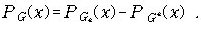제 11 장 Four Color Problem and Knot Theory
3. Four Color Problem
|
|||||||
|
|||||||
Four Color Theorem
(See also: The Mathematics Behind the Maps, The Most Colorful Math of All, and The Story of the Young Map Colorer.)
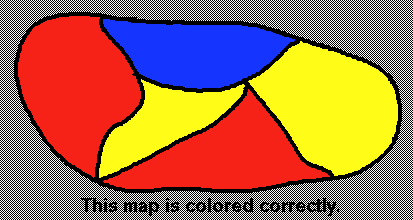
The Four Color Problem was famous and unsolved for many years. Has it been solved? What do you think? The story of the problemSince the time that mapmakers began making maps that show distinct regions (such as countries or states), it has been known among those in that trade, that if you plan well enough, you will never need more than four colors to color the maps that you make. The basic rule for coloring a map is that no two regions that share a boundary can be the same color. (The map would look ambiguous from a distance.) It is okay for two regions that only meet at a single point to be colored the same color, however. If you look at a some maps or an atlas, you can verify that this is how all familiar maps are colored. Mapmakers are not mathematicians, so the assertion that only four colors would be necessary for all maps gained acceptance in the map-making community over the years because no one ever stumbled upon a map that required the use of five colors. When mathematicians picked up the thread of the conversation, they began by asking questions like: Are you sure that four colors are enough? How do you know that no one can draw a map that requires five colors? What is it about the way that regions are arranged and touch each other in a map that would make such a thing true?
When the question came to the European mathematics community at the end of the 19th century, it was perceived as interesting but solvable. Prominent and experienced mathematicians who tackled the problem were surprised by their inability to solve it. Take for example, this account from The Four Color Problem: Assaults and Conquesst by Saaty and Kainen:
A Special Role for the Computer(4색 문제의 해결은 computer를 사용하였다.)
In 1976, the conjecture was apparently proved by Wolfgang Haken and Kenneth Appel at the Univeristiy of Illinois with the aid of a computer. The program that they wrote was thousands of lines long and took over 1200 hours to run. Since that time, a collective effort by interested mathematicians has been under way to check the program. So far the only errors that have been found are minor and were easily fixed. Many mathematicians accept the theorem as true.
The proof of the 4-Color-Theorem is a doorway to some interesting questions about the role of human minds and computing machines in mathematics. Is it ``fair'' to accept as true what a computer can verify, even though no single person can? Does the nature or texture of what humans can discover about their world change with the use of computers as thinking tools? Computers are huge and powerful, but finite; will using them as thinking tools be ultimately limiting? These issues are raised and considered in Ad Infinitum: The Ghost in Turing's Machine by Brian Rotman, and Pi in the Sky by John Barrow.
Statements(명제), Conjectures (가설), and Theorems (정리)
In Mathematics a statement or assertion is a sentence that you are trying to evaluate as true or false. A statement wouldn't have words in it like maybe, perhaps, or sometimes. When you make a statement, you try to make it as precise as possible. When you think that a statement that you have made is true, you call it a conjecture. When you have proved that the statement is true, it is called a theorem.
Writing Down Your Discoveries as Proofs``Doing'' proofs often strikes fear into the heart of the non-mathematician, probably because they are associated with the dense, almost incomprehensible language packed with strange symbols and Greek letters that characterizes the proofs in a math book. It is true that experienced mathematicians communicate the proofs of their theorems in a sparse language that wastes no ink on the page. Inexperienced mathematicians should remember that when they are communicating with one another, completeness, comprehensibility, and understanding are far more important than dense language. What matters the most is showing that the proof has been pursued logically, and that there are no leaps or gaps in the path to the conclusion. Always in mathematics, it is important to ask, ``How do I know this?'' and ``Am I sure that this is true?'' and to communicate the answers to those questions in language that is clear in the mathematical community to which you belong. It is important to remember that proof is not persuasion. Something is not proved mathematically because it seems believable. A statement is true mathematically when, by the rules of logic, it is irrefutable. Understanding the three proof techniques of induction, deduction, and proof by contradiction can often give you ideas for approaches to take when you are struggling with a problem. You can think of these three techniques as patterns of reasoning. These patterns of reasoning are useful in two ways:
Two other techniques, proof by typesetting and proof by intimidation are often used by the unscrupulous. Don't be fooled!
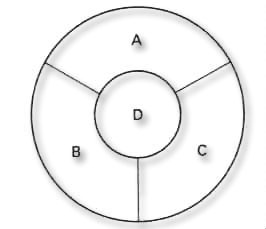
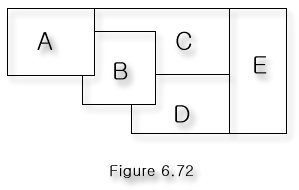
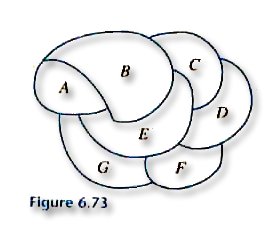
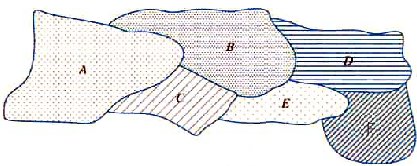
다음 그림의 지도는 그래프의 모양으로 바꾸어 생각할 수 있다.
지도를 색으로 구분할 수 있게 색칠한다는 것은 다음 그래프에서 인접한 vertex는 다른 색을 대응시켜야 한다는 것과 같다. 이것은 graph의coloring문제를 생각하여 해결할 수 있다.
G = (V , E , v) is a graph with no multiple edges and C = { c1,c2,...,cx } is a set of colors. A function f : V → C is called a coloring of graph G using x colors - a coloring is proper if any two adjacent vertices have different colors. - the smallest number of colors needed to produce a proper coloring of a graph G is called the chromatic number of G, denoted by x(G). Chromatic polynomial PG(x) is the number of ways to properly color G with x or fewer color
|