어떤 message를 다른 사람이 알 수 없게 어떤

특정한 사람에게 전달하려고 한다. 이 때 어떠한

방법을 사용하면 효율적인가 생각하여 보시오.

 본 강의에서는 암호이론(coding theory)에 관한

기초적인 이론과 방법에 대하여 학습한다.

     암호이론 (Coding Theory)

암호학(cryptography)는 그리이스 단어로 "hidden"

또는 "secret"을 의미하는 crypto와 writing을

의미하는 grapho를 결합하여 만들어졌으며,

오늘날은 secret writing 또는 code(암호)를

연구하는 학문으로 활발히 연구가 되고 있는

분야이다.

암호학(Cryptography)이란 - plain text를 해독

불가능한 형태로 변형하거나 또는 Cipher text를

해독 가능한 형태로 변환하기 위한 원리, 수단, 방법

등을 취급하는 기술 또는 과학.

종래의 암호시스템(convertional Cryptosystem):

Caesar 암호로부터 DES에 이르기까지 2천여년 이상 사용.

특징 : 송신자와 수신자가 키를 공유

  부호화는 암호화의 단순한 역조작.

Key의 보안유지가 system의 핵심 - Key관리의 어려움 초래.

Public Key Cryptosystem :

암호화 key와 복호화 key를 다르게 작성하여, 암호화 key는

공개키(Public key)로 복호화 key는 비밀키(Secret key)로

하여 Secret Key만 안전하게 유지하는 방식.

특징 :

Key의 안전한 분배 해결. 즉, Key 분배의 필요성이

무실.

관리할 Key의 개수가 적다.

Digital signature가 가능하다. - 신원확인 가능.

암호는 message를 encoding과 decoding하는

과정으로 이루어지며, 송신자와 수신자는 모두 다음을

알고 있어야 한다.

1. symbol과 수 집합 사이의 특수한 대응 관계

2. 특별한 nonsingular matrix A

예를 들어, 25개 정수와 한글 자모음 24와 빈칸은

다음과 같이 대응할 수 있다.

위의 대응 규칙을 사용하면 다음과 같은 message

나는 학교에 간다 는

2 15 2 23 2 v 14 15 1 1 20 80 17 24 v 1 15 2 3 15  

와 같은 숫자 암호로 바뀌었다.

(v은 빈칸 (space key)를 의미한다.)

송신자는 위의 숫자암호를 non-singular matrix A를

사용하여 encode하고, 수신자는 역행렬를 사용하여

decode할 수 있다.

예를 들어, 위의 숫자 암호를 3×6행렬

과 같이 쓸 수 있다.

이 때 encoding matrix  A는 다음과 같은 조건을

갖는 행렬을 택하는 것이 효율적이다.

(1) A는 정칙(non-singular)행렬이다.

(2) A의 모든 원소는 정수이다.

(3) A^-1 의 모든 원소는 정수이다.

  A의 행렬식 값이 1이 된다면 쉽게 위의 조건을

만족하는 encoding matrix를 구할 수 있다.

예를 들어 encoding matrix로

를 택하여 보자. 그러면 우리의 message의

encoding 작업은

encoding된 암호 B는 encoding matrix A를 알지

못하면 그 message가 무엇인지를 알기는 어렵다.

이제 B를 수신한 사람은 원래의 message M을

구하여 원래의 문장으로 바꾸어야 한다.

먼저 M = A^-1 B 이므로

을 수신자가 알고 있으면, decode된 message행렬

M은

M = A^-1 B

이다. 따라서 원래의 송신문장은 다음과 같이 번역될

수 있다.

나는 학교에 간다.

이와 같은 encoding 작업은 행렬의 크기와

encoding 행렬을 어떻게 택하는가에 따라서 달라질

수 있으나, 전송된 문장은 변화가 없음은 분명하다.

주의. 위의 행렬 M을 만들 때, 숫자로 된 암호를 열

벡터로 표시하여 행렬을 만들면 안된다.

 

문제 1. 위의 encoding matrix A를 사용하여 다음 문장을 암호로 고치시오. 박군은 이중첩자다.

 

문제 2.  다음 27개의 정수와 알파벳과 빈칸의 대응관계를 사용하여 영문으로 된 암호를 만들어 봅시다.   0 1 2 3 4 5 6 7 8 9 10 11 12 13 빈칸 a b c d e f g h i j k l m   14 15 16 17 18 19 20 21 22 23 24 25 26 n o p q r s t u v w x y z   그러면 message Send the document today 는 숫자로는 19 5 14 4 0 … 과 같다. 이제 다음과 같은 encoding 행렬 A와 주어진 message를 code로 만들어 보시오.

 

문제 3. 다음 각 경우에 대하여 encoding matrix A와 수신된 code B로부터 암호를 해독하여 보시오.

    본 강의에서는 암호이론(coding theory)에

  관한기초적인 이론과 방법에 대하여 학습한다.

  어떤 message를 다른 사람이 알 수 없게 어떤

특정한 사람에게 특별히 약속한 code로 전달하였다.

 이 때 전송망의 문제로 정확한 전달이 되지 않았다고

한다. 어떻게 하면 잘못 전송된 code를 올바르게

회복할 수 있는지 생각하여 보시오.

 본 강의에서는 암호이론(coding theory) 중에서

error correcting code에 관한 기초적인 이론과

방법에 대하여 학습한다.

An Error-Correcting Code

  Cypher는 국문이나 영문 등을 다른 모양으로

변화시키는 rule을 위미하여 code는 다른 특별한

단어를 대신하는 단어나 기호의 list임을 앞에

학습하였다.

예를 들어 영어로 쓰여진 한글은 encypher 또는

encode되었고 그것을 다시 한글로 번역하는 것은

decypher라고 하며, 한영사전은 code book이 되는

것이다.

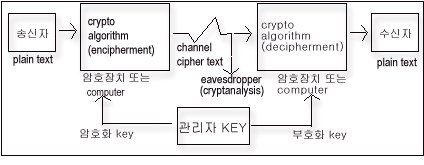
그런데 위 그림에서와 같이 encode된 message를

전송하는 과정 등에서 noise등의 불량 요소가

있으므로 수신자가 받은 code는 원래의 것과는 다를

수 있다. 예를 들어 SHIP을 송출했는데 SHOP을

수신하였다면 송수신자간의 오해가 있을 수 있다.

따라서 송수신된 단어들 간의 closeness에 관하여

알아보기로 합시다.

일반적으로 인공위성이나 컴퓨터 등 사이의

의사전송은 digital 방식의 communication이므로

이진수를 사용하며, message 또는 word는 binary인

n-tuple의 수를 의미한다. 즉 n bit인 정보최소단위를

의미하며 이를 binary string of length n이라고

말하며 단순히  n word라고 부른다.

 

예제 1. ordered 4-tuple ( 0 , 1 , 0 , 1 ) 은 4 bit word이다.

 

예제 2. 십진수 39는 2진법으로는 100111이며 이는 6-tuple ( 1 , 0 , 0 , 1 , 1 , 1 )이다.

 

예제 3. ASC Ⅱ code로 Z는 8-tuple 수 ( 1 , 0 , 0 , 1 , 1 , 0 , 1 , 0 )이다.

x , y 가 두 개의 n-word일 때, 두 단어 사이의 거리

d( x , y ) 를 다음과 같이 약속한다.

d( x , y) : = the number of spots where the two

                words and differ

예를 들면,

x = (0,1,0,1)

y = (0,1,1,1)

이면, d( x , y) = 1 이고 또,

 x = (0,1,1,1,0)

y = (0,1,0,1,1)

이면 d( x , y) = 2 이다.

우리는 d( x , y) 가 거리함수가 됨을 쉽게 증명할 수

있다.

 

문제 1. d( x , y) 가 단어들의 집합에서 거리함수가 됨을 증명 하시오.

일반적으로 단어의 길이가 짧으면 전송이 편하고

noise도 적음은 당연하다. 그렇지만 많고 다양한

message를 보내기는 어렵다. 따라서 전송시 오차도

적고 다양한 message를 보낼 수 있는 optimal

code에 관하여 많은 연구가 이루어지고 있다.

 

정리 1. 만일 단어들이 최소거리가 2t+1이라면 code는 t-error correcting이다. 역으로, 어떤 code가 t-error correcting이면 그 단어들의 거리는 2t+1보다 작을 수는 없다.

증명. 생략 (암호이론 참고도서 참고)

  일반적으로 다음과 같은 조건을 갖는 code에

관하여 생각하여 봅시다.

q : size of the symbol

n : size of the word

t : number of errors corrected

N : number of words in the code

그러면 다음의 관계식을 얻을 수 있다.

 

정리 2.    N.s≤qn 이 때,

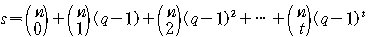
증명.    생략 (암호이론 참고도서 참고)

이 때,N^.s=qⁿ 인 code를 perfect code(완전

암호)라고 부른다.

이제 S를 영벡터 ( 0, 0, …, 0 ) 이 아닌 binary

r-vector들의 집합이라고 하자. 그러면

  ｜S｜= 2^k - 1  

이다. 이 때, H를 열벡터가 S의 모든 원소들로

이루어진 matrix라고 하자.  예를 들면,  r = 3 이면

 

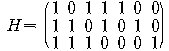
문제 2.  r = 4 일 때의  matrix H 를 구하시오.

x는 n차원의 열벡터라고 할 때,  x' 은 x의

전치행렬(transpose of x)을 나타내기로 합시다.

이제 n-word x' = (x_{1 ,} x_{2 ,}..._, x_n) 에 대하여,

Hamming code C는 다음과 같이 정의된 code이다.

 

C = {x' ｜x' : n-word  이고

x' = (x_{1 ,}x_{2 ,}..._, x_n)

x' ^.H' = O 또는 H ^.x = O }

또, H는 Hamming code code C의 parity check

matrix(기우검사행렬) 이라고 한다.

rank H = r 이므로 위의 Hamming code 의 원소는

          K = n - r = 2^k-1-r

개의  일차독립인 해로부터 생기는 2^k 개의 n-word를

갖는다.

그리고 Hamming code C의 임의의 수 n-words

사이의 거리는 최소 3이다.  따라서, code C는

one-error correcting code가 된다.

 

문제 3.  r = 5 일 때의  Hamming code  C와  parity check matrix H 를 구하시오.

 본 강의에서는 암호이론(coding theory) 중에서

error correcting code에 관한 기초적인 이론과

방법에 대하여 학습한다.