Order Relations and structures
여러 가지 Discrete한 구조들에 관한 여러 이론들
중에서 Order Relations and Structures 에 관하여
학습한다.
그리고 아래의 강의 내용은 B. Kolman, R.C. Bussy
& S. Ross의 저서인
Discrete Mathematical Structures,
Prentice Hall Inc., 1996.
의 7장의 내용을 참고하여 학습하기 바랍니다.
(1) Partially Ordered Sets (Posets)
◆A Relation on a set A is called a partial order
if R is reflexive antisymmetric and transitive.
We denote this poset by (A,R)
◆The poset (A,R-1) is dual of the poset (A,R)
◆If (A,≤) is a poset, the elements a and b of
A are said to be comparable if a≤b or b≤a
◆If every pair of elements in a poset A are
comparable, A is linearly ordered set and
partial order is called a linear order.
Theorem 1. If (A,≤) and (B,≤) are posets,
then (A x B,≤) is a poset with partial order ≤
defined by (a,b) ≤(a',b') if a≤a' in A and
b≤b' in B.
|
◆The partial order ≤ defined on the Cartesian
Product A x B is called the Product partial
order.
◆Define a partial order on A x B, denoted by <
as follows (a,b) ≤(a',b') if a < a' or if a = a'
and b≤b' where but
This ordering is called lexicographic or
dictionary ordering
Theorem 2. The diagram of a partial order has
no cycle of length greater than 1.
|
◆Hasse diagram
From the digraph of a partial order on A ,
Delete all the cycles of length 1.
Delete all the edges that are implied by transitive
property.
Make all edges Point upward so that arrows
may be omitted.
Replace the circles by dots.
Topological sorting
If A is a poset with partial order ≤, we can
find a linear order < such that if a≤b then
a<b.
Constructing such a linear order is called
topological sorting.
Isomorphism
Let (A,≤) and (A',≤') be posets and let f
:A→A' be a one-to-one correspondence
between A and A' . The function is called an
isomorphism from (A,≤) to (A',≤')
if for any a and b in A .a≤b if and only if
f(a)≤'f(b)
Theorem 3. (Principle of Correspondence)
Let : be an isomorphism from (A,≤) to
(A',≤') and B∈A and B'∈f (B).
If the elements of B have any property relating
to one another or to other elements of A ,
and if this property can be defined entirely in
terms of the relation ≤, then the elements of
B' must possess exactly the same property,
defined in terms of ≤.
|
◆Hasse diagram of (A,≤) becomes Hasse
diagram of (A',≤') if each label a is replace by
f (a).
문제 1. Show that if R is a linear order on
the set A, then R-1 is also a linear order on
A.
|
(2) Extremal Elements of Partially
Ordered Sets
◆Let (A,≤) be a poset.
- an element a∈A is called maximal
element of A if there is no element c in A
such that a≤c
- an element b∈A is called minimal
element of A if there is no element c in A
such that c≤b
Theorem 1. Let A be a finite nonempty poset
with partial order ≤. Then A has at least one
maximal element and at least one minimal
element .
|
◆Let (A,≤) be a poset
- an element a∈A is called a greatest
element of if x≤a for all a∈A
- an element a∈A is called a least element
of A if a≤x for all a∈A
Theorem 2. A poset has at most one greatest
element and at most one least element.
|
◆Let (A,≤) be a poset and B⊆A.
- an element a∈A is called an upper
bound of B if b≤a for all b∈B
- an element a∈A is called an lower bound
of B if a≤b for all b∈B
◆Let A be a poset and B⊆A.
- an element a∈A is called a least upper
bound (LUB) of B if a is an upper bound of
B and a≤a' whenever a' is and upper
bound of B
- similarly an element a∈A is called a
greatest lower bound (GLB) of B if a is a
lower bound of B and a'≤a whenever a' is
a lower bound of B
(3) Lattices
◆A lattice is a poset (L,≤) in which every
subset {a,b} has a LUB and a GLU.
we denote LUB({a,b}) by and GLB({a,b}) by
a∧b
Theorem 1. If (L1,≤) and (L2,≤') are lattices,
then (L,≤) is a lattice, where L = L1 x L2 , and
the partial order ≤ of L is the product partial
order.
|
◆Let (L,≤) be a lattice. A nonempty subset S
of L is called a sublattice of L if a∨b∈S and
a∧b∈S whenever a∈S,b∈S
◆If f : L1 →L2 is an isomorphism from the
poset (L1,≤1) to the poset (L2,≤2) then L1 is
a lattice if and only if L2 is a lattice
If two lattices are isomorphic, they are
isomorphic lattices
◆A lattice L is said to be bounded if it has a
greatest element I and a least element O
Theorem 5. Let L =
{a1 , a2 , ... , an } be a finite lattice Then L is
bounded.
|
◆A lattice L is called distributive if for any
elements a,b,c in L
◆Let L be a bounded lattice with greatest
element I and least element O and let a∈L .
An element a'∈L is called a complement of a
if a∨a'=I and a∧a'= O
Theorem 7. Let be a bounded distributive
lattice. If a complement exists, it is unique.
|
◆A lattice L is called complemented if it is
bounded and if every element in L has a
complement.
문제 2. Show that a subset of a linearly
ordered poset is a sublattice.
|
(4) Finite Boolean Algebras
Theorem 1. If S1={x1 , x2 , ... , xn} and
S2={y1 , y2 , ... , yn} are any two finite sets
with elements, then lattices (P(S1),⊆) and
(P(S2),⊆) are isomorphic.
|
Proof: for each subset A of 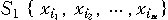 , let , let 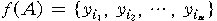 The The
point is that the lattice (P(S),⊆) is completely
determined as a poset by the number |S |.
◆If the Hasse diagram of the lattice
corresponding to a set with n elements is
labeled by sequences of 0's and 1's of length
n, then the resulting lattice is named by Bn
- If x = a1, a2 , ... , an and y = b1, b2 , ...
, bn are two elements of Bn
1. x≤y iff ak≤bk (as numbers 0 or 1)
for k = 1,2,...,n
2. x∩y = c1, c2 ,...,cn where ck = min{ak ,bk }
3. x∪y = d1, d2 ,...,dn wheredk = max{ak ,bk }
4. x has a complement x' =z1, z2 ,...,zn
where zk = 1 if xk = 0 and zk = 0 if xk = 1
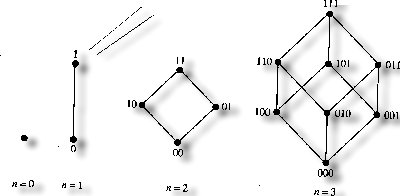
◆The following figure shows the Hasse
diagrams of the lattices Bn for n=0,1,2,3
◆A finite lattice is called a Boolean algebra
if it is isomorphic with Bn
Theorem 2. Let n = p1, p2, ... ,pn where the
pi are distinct primes, then Dn is a Boolean
algebra.
|
Theorem 3. (Substitution Rule for Boolean Algebra)
Any formula involving ∪,∩ or that holds for
arbitrary subset of a set S will continue to
hold for arbitrary elements of a Boolean
algebra L if
∧ is substituted for ∩, and ∨ for ∪.
|
Theorem 4. for any n≥1, Bn is the product
BxBx...xB of B(B=B1 factors , where
BxBx...xB is given the product partial order.
|
문제 3. Are there any Boolean algebras having
three elements ? Why or why not ?
|
|