Relations and Digraphs
¿©·¯ °¡Áö DiscreteÇÑ ±¸Á¶µé¿¡ °üÇÑ ¿©·¯ À̷еé Áß¿¡¼
¸ÕÀú
relation°ú digraph¿¡ °üÇÏ¿© ÇнÀÇϵµ·Ï ÇսôÙ.
±×¸®°í ´ÙÀ½ÀÇ °ÀÇ ³»¿ëÀº B. Kolman, R.C. Bussy & S.
RossÀÇ Àú¼ÀÎ
Discrete Mathematical Structures,
Prentice Hall Inc., 1996.
ÀÇ 5ÀåÀÇ ³»¿ëÀ» Âü°íÇÏ¿© ÇнÀÇϱ⠹ٶø´Ï´Ù.
(1) Product Sets and Partitions
¡ßOrdered pair (a,b) is a listing of objects a and b in
a prescribed order
¡ßProduct Set (Cartesian Product):
For two nonempty set A and B
A x B = { (a,b) | a¡ôA ,b¡ôB }
(Example) Let A = {1, 2, 3}, B = {r,s}; then
A x B = {(1,r) , (1,s) , (2,r) , (2,s) , (3,r) ,(3,s)}
|
¡ßGeneralization of Cartesian product
A1 x A2 x , ..., x Am of the nonempty sets A1,
A2 , ..., Am is defined as
{(a1, a2 , ..., an) | ai¡ôAi , i = 1, 2, ... ,m }
¡ßA Partition or quotient set of a nonempty set A is
a collection P of nonempty subsets of A such that
1. Each element of A belongs to one of the
sets in P
2. If A1 and A2 are distinct element of P then
A1 ¡û A2 = ¨ª
- P¡ö P(A) , that is a partition of a set A is a
subset of the power set of A
(2) Relations and Digraphs
¡ßA relation R from A to B is a subset of
A x B
- If R ¡öA x B and , (a,b)¡öR ,
a is related to b by R and we write
a R b
(Example) Let A = B = {1, 2, 3}.
Define a relation R as follows
a R b iff a < b
Then R ={( 1, 2 )( 1, 3 )( 2, 3 )}
|
¡ßIf R ¡öA x A then R is said to be a relation
on A
¡ßLet R ¡öA x B
- Domain of R : the set of elements in A
which are related to some elements in B
- Range of R : the set of elements in B which
are related to some elements in A
-R-relative set of x ,
R(x) = { y¡ôB |x R y }
- if A1 ¡ö A then R -relative set of A1 ,
R(A1)={y¡ôB | x R y for some x in A1}
(Example) A = B = {a,b,c,d} ,
R = {(a,b) (a,d) (b,c) (c,a)}
Dom (R)={a,b,c} Ran (R)={a,b,c,d}
R(a)={b,d} R{(b,c)} = {a,c}
|
¡ßThe matrix of a Relation
- If A = {a1, a2, ..., an} B = {b1, b2, ..., bn}
and R ¡ö A x B
we can represent R by mxn matrix MR=[mij]
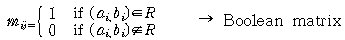
(Example) A = {a,b} B={1,2,3}
R={(a,1)(b,2)(b,3)} then
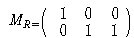
|
¡ßLet R ¡öA x A
- Digraph of
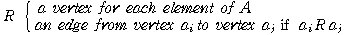
¡ßLet a¡ô A then the indegree of a is the number of
b¡ô A such that (b,a) ¡ôR
the outdegree of a is the numberof b¡ô A such that
(b,a) ¡ôR = |R(a)|
(3) Paths in Relations and Digraphs
¡ßLet R be a relation on a set A
A path of length n in R from a to b is a finite
sequence ¥ð=a ,x1, x2 , ... , xn-1 , b
such that a R x1, x1 R x2 , ... , xn-1 R b
A path that begins and ends at the same vertex is
called a cycle.
¡ßDefine Rn as follows : x Rn y means that there is
a path of length n from x to y in R
- R¡Ä is defined as follows :x R¡Ä y means that
there is a path from x to y in called
"connectivity relation"
Theorem 1. Let's define the Boolean product of A
and B (A¢ÁB ) to be
C=[cij] such that
cij = 1 if aik =1 and bkj = 1 for some k
0 otherwise
Then 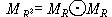 ( MR¢ÁMR = (MR)O2 ( MR¢ÁMR = (MR)O2
|
Theorem2.

|
Proof : By the induction, we can prove
Theorem 2.
¡ß 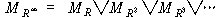
¡ßReachability relation R* of R is defined as follows
:
x R*y means that x = y or x R¡Äy
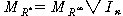 where In is the n x n Identity
matrix where In is the n x n Identity
matrix
(4) Properties of Relations
¡ßReflexive and irreflexive relations
- A relation R on a set A is reflexive if (a,a) ¡ô R
for all a ¡ô A
- A relation R on a set A is irreflexive if (a,a) 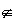 R
for all a ¡ô A R
for all a ¡ô A
(Example) A = {1,2,3,4}
a R b iff a¡Âb ¡æ reflexive
a R b iff a<b ¡æ irreflexive
|
¡ßSymmetric, asymmetric and antisymmetric relations
- A relation R on a set A is symmetric
if whenever a R b then b R a
- A relation on a set is asymmetric
if whenever a R b then ~b R a
- relation R on a set A is antisymmetric if
whenever a R b and b R a then a = b
(Example) A = {1,2,3,4}
R = {(1,2)(2,2)(3,4)(4,1)}
R is not symmetric, not asymmetric
since (2,2)¡ôR, but antisymmetric
|
¡ßProperties of matrix
- The matrix MR = [mij] of a symmetric relation
satisfies the property that
if mij =1 then mji =1
Therefore 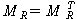 so that MR is a symmetric
matrix so that MR is a symmetric
matrix
- The matrix MR = [mij] of an asymmetric
relation R satisfies the property that if mij =1
then mij =0
- The matrix MR = [mij] of an antisymmetric
relation R satisfies the property that if i ¡Á j
then mij =0 or mji =0
¡ß In the digraph of a symmetric relation R , if two
vertices are connected by an edge they must always
be connected in both direction.
If we replace these two edges with one undirected
edge the resulting diagram is called graph of the
symmetric relation.
¡ßsymmetric relation R on a set A will be called
connected if there is a path from any element of A
to any other element of A
¡ßTransitive relations
-A relation R on a set A is transitive if whenever aRb
and bRc then aRc
(Example) A=Z
aRb iff a<b then R is transitive
|
Theorem 1. A relation R is transitive iff it satisfies
the following property :
If there is a path of length greater than 1 from a to
b, then there is a path of length 1 from a to b.
|
(5) Equivalence Relations
¡ßA Relation R on a set A is called equivalence
relation if it is reflexive. symmetric and transitive
Exampe. Let A = and
{ (a,b) ¡ô A x B |2 divides a-b }
We write aRb as a¡Õb (mod 2) read "a is congruent
to b mod 2"
Show that R is an equivalence relation
Proof. First a¡Õa (mod 2) since 2 divide a-a = 0
second if a¡Õb (mod 2) then b-a = 2(-k) hence
a¡Õb (mod 2) . Finally, suppose that a¡Õb (mod 2)
and b¡Õc (mod 2) then a-b = 2k1, and b-c = 2k2
adding the two equations yields a-c = 2( k1 + k2 )
Hence (mod 2)
Theorem 1. Let P be a partition of a set A ,
and aRb iff a and b are members of the same
block. Then R is an equivalence relation on
A¡æR is called the equivalence relation
determined by P
|
Lemma 1. Let R be an equivalence relation on
A and let a¡ôA, b¡ôA then
aRb iff R(a) = R(b) |
Proof. (i) Suppose R(a) = R(b), since R is reflexive
b¡ôR(b),
therefore b¡ôR(a), so aRb
(ii) Suppose aRb , b¡ôR(a) and since R is symmetric
a¡ôR(b), let x¡ôR(b) then since R is transitive and
b¡ôR(a), x¡ôR(a) ¡æR(b)¡öR(a)
let x¡ôR(a) , in the similar way x¡ôR(b)¡æR(a)¡öR(b).
Therefore we have
R(a) = R(b).
Theorem 2. Let R be an equivalence relation
on A and let P be the collection of all distinct
relative sets R(a) ,a¡ôA then P is a partition
of A and R is the equivalence relation
determined by P.
|
Proof. We must show the following Properties.
(a) Every element of A belong to some relative
set.
(b) It R(a) and R(b) are not identical then R(a)
¡û R(b) = 0
(a) is true since R(a) = 0 by reflexivity of R
(b) is equivalent to "If R(a) ¡û R(b) ¡Á0 then
R(a) = R(b)."
Assume that c¡ô R(a) ¡û R(b) then aRc and
bRc, since R is symmetric cRb.
By the transitivity aRb
Then R(a) = R(b) by Lemma 1.
(6) Computer representation of
Relations and Digraphs
Refer the pp. 136-145 of the book :
B. Kolman, R.C. Bussy & S. Ross,
Discrete Mathematical Structures,
Prentice Hall Inc., 1996.
(7) Manipulation of Relations
¡ßLet R and S be relations from A to B then R, S ¡öA
x B
- complement of 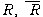 is defined by is defined by 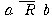 if
and only if a R b' if
and only if a R b'
- R¡ûS : Intersection of R and S
- R¡úS : Union of R and S
- inverse of R , R-1 is defined by b R-1a if and
only if a R b
Dom(R-1) = Ran(R) , Ran(R-1) = Dom(R)
-MR¡ûS = MR¡ü MS
-MR¡úS = MR ¡ýMS
-MR-1 = (MR )T
-
¡ßClosures
- The closure of R with respect to a Property : the
smallest relation R1 that contains R and possesses
the Property
¡ßComposition
- Let R ¡öA x B, S ¡öB x C
composition of R and S is defined as follows.
a(R°° S)b if a R b and b R c for some b¡ôB
- Let R and S be relations on A
then MR°° S= MR¢ÁMS
Theorem 1. Let R¡öA x B, S ¡öB x C,
T ¡öC x D. Then
T°°( S°° R ) = (T°° S)°° R
|
Proof. MT°°( S°° R ) =MS°° R¢ÁMT =(MR¢Á
MS)¢ÁMT
M(T°° S°)°° R =MR¢ÁMT °S¢ÁMT =MR¢Á( MS¢ÁMT)
(8) Transitive Closure and
Warshall's Algorithm
Theorem 1. Let R be a relation on A
then R¡Ä is the transitive closure of R.
|
Proof.R¡Ä is transitive since if a R¡Ä b and b R¡Ä c
then a R¡Ä c
We must show that R¡Ä is the smallest transitive
relation containing R
Let S be any transitive relation on A and R¡öS
Since S is transitive, 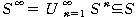
Since R¡öS , R¡Ä¡öS¡Ä , Therefore R¡Ä¡öS¡Ä ¡öS
Theorem 2. Let A be a set with |A| = n and
let R be a relation on A. Then
R¡Ä= R ¡úR2 ¡ú... ¡úR*.
|
Proof. The length of the shortest path from i to j
cannot be more than n-1.
¡ßWarshall's Algorithm
- an efficient method for finding the transitive
closure of a relation R on a set A
- let R be a relation on a set A = {a1 , a2 , ... , an}
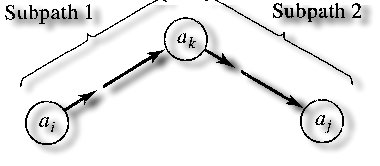
- let x1 , x2 , ... , xm be a path in R then
x2 ,x3 ,...,xm-1 are interior vertices of the path.
- we define a Boolean matrix Wk as follows ; Wk[ij]
= 1 iff there is a path from ai to aj in R whose
interior vertices come from the set {a1 , a2 , ... , an}
then 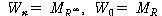
- suppose that Wk [tij] and Wk-1 [sij]
tij = 1 iff (1) sij = 1 or
(2)sik = 1 and skj = 1
The Algorithm of Warshall
1. closure ¡ç Mat
2. For K= 1 to N
3. For I = 1 to N
For J = 1 to N
closure[I,J ] = closure[I,J]¡ý ( closure[I,K]¡ü
closure[K,J] )
end of algorithm Warshall.
|