Eulerian Graph and Hamiltonian Graph
그래프이론 중에서 가장 중요한 문제는 주어진그래프
에서 어떤 원하는 행로나 cycle 등을 찾는 방법이다.
우리는 이것을 학습하기 전에 기본적인 그래프
용어를 다시 알아보도록 합시다.
정의 1. 무방향 그래프 G에서 한 정점 v의 차수
(degree)는 정점 v에 연결되는 모서리의 개수이다.
정점 v의 차수를 deg(v)로 표시하며, deg(v)는 정점
v에 연결된 모서리의 수이다.
|
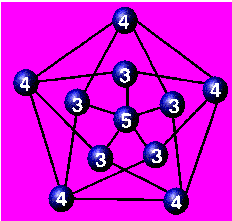
다음 그래프에서 정점에 표시된 수는 각
정점의 degree(차수)를 나타낸다.
정의 2. 단순 방향 그래프 G =< V , E >에서 한
정점에 대하여 정점 v를 출발점으로 갖는 모서리의
수를 v의 외부 차수(outdegree)라고 하며, v를
도착점으로 갖는 모서리의 수를 v의 내부 차수(
indegree) 라고 말한다. 내부와 외부 차수의 합을 총
차수 (total degree) 라고 말한다.
|
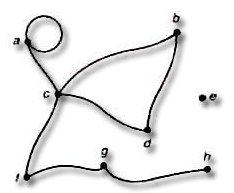
문제 1. 다음 그림에서 각 정점의 degree를
구하시오.
 |
이제 모든 vertex v에 대한 deg(v)의 합을 구하여
봅시다.
임의의 무방향 그래프 G에서 임의의 모서리(a,b)에
대하여,
각각의 deg(a)와 deg(b)의 수는 중복하여 더하게
된다.
결국 G =( V , E )가 무방향 그래프라면
모든 vertex v에 대한 deg(v)의 합은
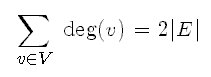
와 같이 전체 모서리의 수에 2 배와 같다.
정리 1. G =( V , E )가 무방향 그래프일 때,
모든 vertex v에 대한 deg(v)의 합은
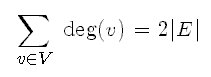
이다. |
문제 2. 임의의 무방향 그래프에 대해, 홀수 차수를
갖는 정점의 수는 짝수임을 증명하시오.
|
각 정점이 같은 차수를 갖는 무방향 그래프를
정규(regular)그래프라고 하였다.
이 때, 정리 1의 응용으로 우리는 다음과 같은 문제를
생각하여 봅시다.
모든 정점이 차수 4를 갖고 전체 10개의 모서리를
갖는 정규그래프가 존재할 수 있는가 ?
우리는 이를 해결하는 도구로 정리 1을 사용할 수
있다.
즉, 2|E|= 20 = 4|V|이어야 하므로 차수
4인 5개의 정점을 갖는 그래프가 존재한다.
다음 그림은 위 조건을 만족하는 2 개의 비동형
그래프이다.
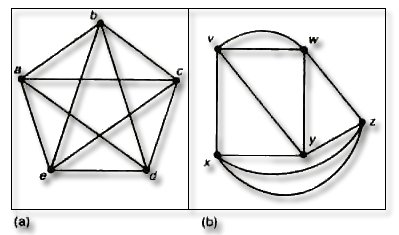
문제 3. 모든 정점의 차수가 3인 20개의 모서리를
갖는 regular 그래프는 존재하는가 알아보시오.
|
이제 Euler의 Konigsberg의 다리문제를 해결하기
위하여 각 정점에서의 차수를 사용하여 봅시다.
앞 절에서 학습하였듯이, Konigsberg 도시는
Pregel강에 의하여 4개의 구역으로 나누어졌다.
다음 그림처럼 ,이 지역은 7개의 다리로
연결되어있었고 주민들은 어느 점을 시작하여
산책하면 한 번 지나간 다리는 다시 거치지 않고
7개의 다리를 전부 산책할 수 있는가를 항상
궁금하게 생각하였다고 한다.
이 때 Euler라는 대수학자가 정점의 차수를 이용하여
해결할 수 있었으며, 이것이 곧 그래프이론 (graph
theory) 의 시작이었던 것은 앞에서 말한바 있다.
이러한 문제를 해결하기 위하여, Euler는 그림 2처럼
그래프의 정점과 간선을 이용하여 간단하게
표현하였고. 여기서 각각의 정점의 차수는
deg(1) = deg(2) = deg(3) = 3, deg(5) = 5.
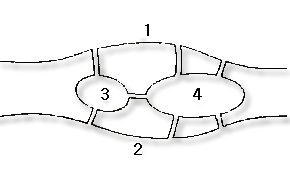 그림 1 그림 1
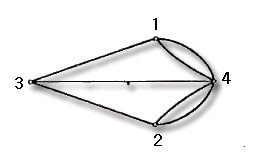 그림 2 그림 2
위 그림에서 1과 2는 강의 양쪽 기슭을 의미하며,
3과 4는 2개의 섬을 나타낸다. 이 점들을 연결하는
7개의 선들은 7개의 다리를 나타낸다.
위 문제의 해결은 그래프에서 홀수 차수의 정점의
수에
달려있다는 것을 Euler는 발견했다.
정의 3. G =( V , E )를 무방향 그래프라고 하자.
만일 각각의 모서리를 정확하게 한 번씩 경유해서
그래프의 모든 모서리를 지날 수 있는 경로가
존재한다며, 그래프 G 는 Euler경로 (Euler path)를
갖는다고 한다. 또, Euler circuit 이란 Euler
경로로서 circuit인 것을 의미한다.
|
이제 Graph이론의 가장 중요한 정리를 학습하도록
합시다
정리 2. G =( V , E )를 무방향 그래프라고 하자.
이 때 그래프 G가 Euler 경로를 갖기 위한 필요충분
조건은 그래프 G가 연결된 그래프이며, 모든 정점의
차수(degree)가 짝수인 것이다.
|
증명. 위 정리의 증명은 그래프이론에 대한 표준적인
교재들을 참고하여 학습하기 바랍니다.
정리 3. G =( V , E )를 무방향 그래프라고 하자.
(1) If a graph G has more than two vertices
of
odd degree, then there can be no Euler path
in G.
(2) If G is connected and has exactly two
vertices of odd degree, there is an Euler Path
in G.
Any Euler path in G must begin at on vertex
of odd degree and end at the other.
|
문제 4. 다음 그래프에서 Euler Path를 찾아
보시오.
(1)
(2)
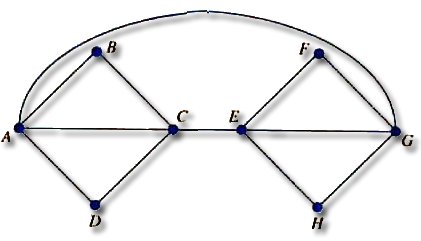
(3)
|
Euler경로는 주어진 그래프에서 모서리에 관한
경로를 발견하였지만 , Euler는 모든 정점을 경유하는
경로에 대하여 다루지 않았다.
여기서 우리는 연결된 그래프가 각 정점을 정확히
한번만 경유하는 경로를 갖고 있는지를
생각하여봅시다.
이와 같은 문제는, salesman의 여행 등과 같이
경제적으로 의미있는 응용문제이다.
즉, 정점들은 방문할 도시들을 나타냈으며, 이 게임의
목적으로는 각 도시를 정확히 한 번만 경유하는
최적의 sales 여행경로을 발견할 수 있는가하는
문제이다.
연결된 그래프가 각 정점을 정확히 한번만 경유하는
경로인 한 circle(순환)을 아일랜드의 수학자
Hamilton (Sir William Rowan Hamilton, 1805 -
1865)의 이름을 따서 Hamilton 순환 (Hamiltonian
cycle) 이라고 부르며, Hamiltion 순환을 갖는 모든
그래프를 Hamilton 그래프(Hamiltonian graph)라고
한다.
즉, 그래프 G =( V , E )가 주어진 모든 정점들을
정확하게 한번만 경유해서 하나의 경로가 있는
그래프를 우리는 Hamilton경로가 존재한다고 한다고
한다.
더욱이 그래프에서 모든 정점들을 포함하는 사이클을
우리는 Hamilton 사이클이라고 하며, 한 모서리를
제외한 경로를 우리는 Hamilton 경로라고 한다.
주어진 그래프 G =( V , E )에서 , Hamilton경로가
있는가를 확인하려면 다음을 검토하여야 한다.
1. 만일 그래프 G가 Hamiltion 경로를 갖는다면, V에
속한 모든 정점들의 차수는 2보다 크다. 즉 deg(v)
≥2.
2.만일 V에 속하는 정점 a에 대해 deg(a) =2 이면,
정점 a에 연관된 두 개의 모서리들은 당연히 그래프
G에 대한 Hamilton경로에 속하는 모서리이다.
3. 만일 V에 속하는 정점 a에 대해 deg(a) = 2 이면,
정점 a에 연관된 두 개의 모서리는 그래프 G의
Hamilton 경로에 속하는 간선에서 제외된다.
4. 그래프 G에서 Hamilton 경로를 찾는 과정에서 ,
그래프의 모든 정점들을 포함하지 않는 부분
그래프에서 경로를 얻을 수 없다.
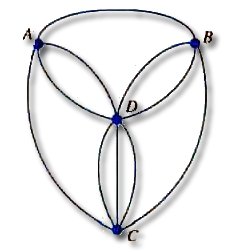
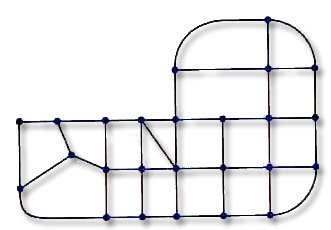
문제 5. 다음 그래프에서 Hamilton 경로를
찾아 보시오.
(1)

(2)
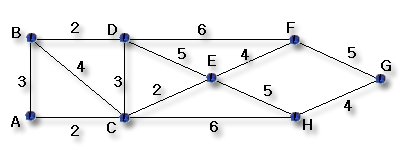
|
이제 끝으로, 우리는 더욱 일발화된 정리로 다음을
소개한다.
정리 4. 만약 G =( V , E )가 n≥3인 정점을 갖는
단순 그래프라고 할 때, 서로 인접하지 않는 두 정점
u와 v사이에 식
deg(u) + deg(v) ≥ n
이 성립하면, 그래프 G는 Hamilton 경로를 갖는다.
|
증명. 위 정리의 증명은 그래프이론에 대한 표준적인
교재들을 참고하여 학습하기 바랍니다.
따름정리. G has a Hamiltonian circuit if each
vertex
has degree greater than or equal to n/2.
|
정리 5. 그래프 G =( V , E )가 n≥3인 정점을 갖는
단순 그래프라고 할 때, 모든 정점 v에 대해 다음
부등식
deg(v)≥2
을 만족하면, 그래프 G는 Hamilton경로를 갖는다.
|
정리 6. Let the number of edges of G be m.
Then
G has Hamiltonian circuit if m is equal to or
greater
than 1/2 (n2 - 3n + 6), where n is the number
of
vertices of G.
|
Graph Theory Reference Links
This is the home page for a series of short interactive
tutorials introducing the basic concepts of graph theory.
They are designed with the needs of future high school
teachers in mind and are currently being used as a
supplement to our Mathematical Modeling course (Math
451).
These tutorials are created using the Web Tutor so that
most of the pages of this tutorial require that you pass a
quiz before continuing to the next page, while others ask
for a written comment. The Web Tutor must be able to
keep track of your progress, so you will need to register
for each of these courses by pressing the [REGISTER]
button on the bottom of the first page of each tutorial.
(You can use the same username and password for each
tutorial, but you will need to register separately for each
course.)
Introduction to Graph Theory (6 pages)
Starting with three motivating problems, this tutorial
introduces the definition of graph along with the
related terms: vertex (or node), edge (or arc), loop,
degree, adjacent, path, circuit, planar, connected and
component. [Suggested prerequisites: none]
Euler Circuits and Paths
Beginning with the Königsberg bridge problem we
introduce the Euler paths. After presenting Euler's
theorem on when such paths and circuits exist, we
then apply them to related problems including pencil
drawing and road inspection. [Suggested
prerequisites: Introduction to Graph Theory]
Coloring Problems (6 pages)
How many colors does it take to color a map so that
no two countries that share a common border have
the same color? This question can be changed to "how
many colors does it take to color a planar graph?" In
this tutorial we explain how to change the map to a
graph and then how to answer the question for a
graph. [Suggested prerequisites: Introduction to
Graph Theory]
Adjacency Matrices (Not yet available.)
How do we represent a graph on a computer? The
most common solution to this question, adjacency
matrices, is presented along with several algorithms
to find a shortest path... [Suggested prerequisites:
Introduction to Graph Theory]
Related Resources for these Tutorials:
Other Graph Theory Resources on the Internet:
|