Graph의 정의
그래프 이론(graph theory)을 이용한 문제 해결은
1736년 스위스의 수학자 Leonard Euler(1707-83)에
의하여 최초로 시작되었다. 당시 러시아의
Konigsberg에는 그림 1처럼 Pergel 강에 있는 두
개의 섬과 일곱 개의 다리로 구성된 산책할 수 있는
공원이 있었다. 이곳 시민들은 자주 산책을 즐기면서
이들은 집에서 출발하여 정확하게 일곱 개의 다리를
산책하는데 지나간 다리는 다시 지나지 않는 방법으로
이어지는 산책경로가 존재하는지 궁금하게
생각했었다. 그런데 Euler는 그림 2의 단순화된
그래프 이론을 이용하여 이 문제를 쉽게 해결할 수
있었다.
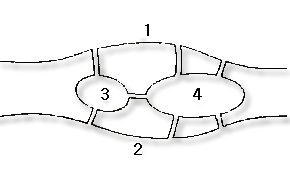 그림 1 그림 1
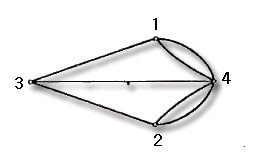 그림 2 그림 2
1과 2는 강의 양쪽 기슭을 의미하며, 3과 4는 2개의
섬을 나타낸다. 이 점들을 연결하는 7개의 선들은
7개의 다리를 나타낸다. 여기서 Euler는 이 문제를
다음과 같은 방법으로 설명하였다.
1,2,3,4 중 어느 한 위치에서 시작해서 각 다리를
정확하게 한번만 산책하는 방법으로 출발했던 위치로
되돌아 오는 것이 가능할까?
이 문제에 대한 해답은 뒤에서 학습할 Euler와
Hamilton경로의 이론에서 알 수 있을 것이다.
Euler는 주어진 그래프에서 정점의 차수(degree)가
짝수를 갖고 있을 때, 이 문제가 해결됨을 수학적
증명으로 보였다.
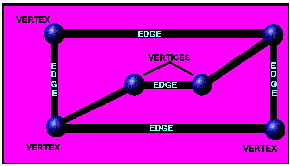
위의 그림 2와 같은 도형을 그래프(graph)라고
부르며, 각 점들을 정점(vertex) V로, 다리와 도로를
모서리(edge) E로 표현되는 그래프 G = (V, E)라고
하며, 이러한 그래프이론은 1736년 Euler의 논문에서
처음 발표되었다.
그래프 이론은 수학의 가장 성공적인 응용 부분의
하나이며, 이것은 전산학, 물리학, 화학, 공학,
의학,생물학, 심리학, 경제학, 도시계획, 인공지능학,
언어학 등의 다른 여러 분야에서 중요한 응용을 갖고
있다.
다음의 강의 내용은 그래프이론에 대한 표준적인
교과서를 참고하여 학습하기 바랍니다.
정의 1. V를 공집합이 아닌 정점(vertex)들의
집합이라고 하고 모서리(Edge)들의 집합을
E⊆V×V라고 하자 .
이 때, 우리는 G = < V, E > 를 방향그래프(digraph
또는 directed graph)라고 하며, 방향이 없는
그래프는 단순히 G = ( V, E )로 표시하기로 한다.
그래프 G에서 다른 정점들과 연결되지 않은 정점 v을
고립정점이라고 하고, 고립정점으로만 이루어진
그래프를 공 그래프 (null graph)라고 한다.
|
그래프 G = (V, E)에서 V와 E는 유한한 원소들의
집합으로 가정한다.
임의의 모서리 x ∈ E 가 V의 순서쌍 <u, v> 혹은
비순서쌍 (u, v)와 연관이 있을 때, 모서리 x는 정점
u 와 v를 연결(connect)한다고 말하고, 임의의
모서리에 의하여 연결된 정점들의 쌍을 인접한
정점(adjacent vertices)들이라 한다. 방향 그래프를
나타낼 때, 정점은 점 a, b, c 등으로 표시하며
모서리는 <a,b>, <a,c> 등으로 표시한다.
다음과 같은 용어를 알아봅시다.
Three properties of graphs that are
important in many problems are size,
regularity, diameter.
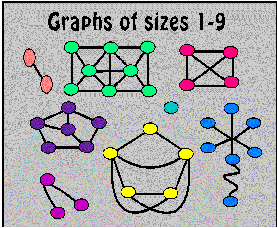
The size of a graph is the number of
vertices it has.
다음 그래프는 size가 1부터 9 까지인
graph를 나타낸다.
Just like the diameter of a circle measures
the distance across a circle, diameter is a
measure of distance between vertices in a
graph. The idea of "distance" in a graph is
different from the "distance" we commonly
measure with a tape measure, however,
because we can stretch or shrink the
edges of a graph to be any length at all.
Imagine traveling from vertex to vertex
along the edges of a graph. Each trip
along one edge, no matter how long or
short the edge happens to be, counts as
one move. The distance from one vertex
to another is the smallest number of
moves that it takes to get there.
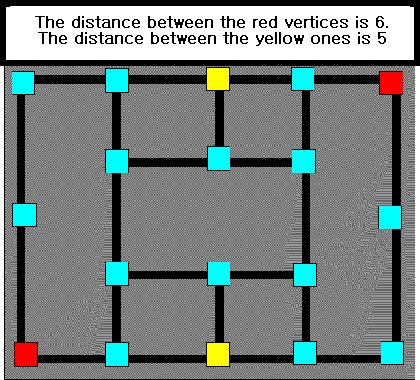
The diameter of a circle measures the
distance between two points on the circle
that are farthest apart. Similarly, the
diameter of a graph is the distance
between the two vertices of the graph that
are farthest apart.
예제 1. 그림 3의 그래프는 다음 성분을 갖는다 .
모서리의 집합 E = { < a , a >, < a , b >,
< a , d> , < b , c >}
정점의 집합 V = { a , b , c , d , e }
 그림 3 그림 3
|
방향 그래프 G = <V, E> 에서 x ∈ E 가 두 정점의
순서쌍 <u, v> 로 연결된 방향이 있는 모서리일 때,
모서리 x 는 u 를 출발점 (initial vertex) , v를
도착점 (terminal vertex ) 이라고 한다. 방향
그래프에서 , 모서리는 화살표로 표시한다.
무방향 그래프(undirected graph)의 모서리는
(a , b ), ( b , c ) , ( a , a ), ( a , d ) 등과 같으며
일반적인 모서리 ( a , b )는 두 개의 방향성 모서리
{< a , b >,< b , a>} 를 의미한다. 여기서,
(a , b ) = (b , a )이면 a = b 가 된다.
정의 2. 평행한 모서리가 존재하지 않는 그래프를
평면그래프(planar graph 또는 simple graph)라고
하며, 평행한 모서리들이 존재한다면
비평면그래프(nonplanar 또는 multigraph)라고
말한다.
|
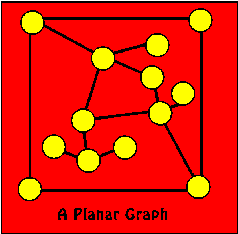 그림 4(1) 그림 4(1)
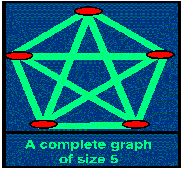 그림 4(2) 그림 4(2)
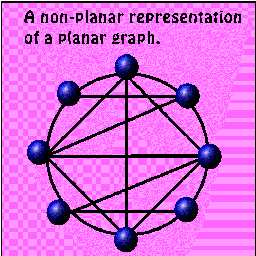 그림 4(3) 그림 4(3)
그림 4(1)는 평면그래프의 예, 그림 4(2)는
비평면그래프의 예이고, 그림 4(3)은 평면그래프를
비평면그래프로 그린 예이다.
이제 그래프의 성질에 대하여 정의하여 봅시다.
정의 4. 그래프 G = (V, E)에서 요소
(components)의 수는 연결된 그래프의 수를
의미하며, k(G)로서 나타낸다.
|
예제 3. 다음 그림 5(a)는 전체가 연결된 그래프이기
때문에 K(G1) = 1 이지만, 그림 5(b)는 두 개의 독립
연결 그래프이므로 K(G2) = 2이다.
|

|