Fibonacci 수열과 점화식 II
이제 Pascal의 삼각형을 이용하여 Fibonacci 수열의
일반항과 여러 성질에 관하여 학습하도록 합시다.
Fibonacci sequence와 이와 관련된 문제를 통하여 탐구적
방법으로 점화식에 대하여 알아보도록 합시다.
제 6주 강의록은 영문으로 작성되었습니다. 국문강의록 보다 읽기가
조금 어렵기 때문에 여러분들은 천천히 읽고 학습하기 바랍니다.
Generalization :
If n represents the total number of M and S books to be
shelved under these conditions, then the total number of
possible arrangements for n books, n>1, is
F(n)=F(n-1)+F(n-2), where F(0)=1 and F(1)=2.
Justification :
To justify that this relationship holds in general, consider the
shelving possibilities when there are n M and S books.That is,
we are looking for F(n). There are two distinct cases to
consider:
Case I: The first (leftmost) book is a M book.
If the first book is a M book, there are F(n-1) ways to arrange
the remaining n-1 books, for the next book on the shelf can be
either M or S.
Case II: The first (leftmost) book is a S book.
If the first book is a S book, there are F(n-2) ways to arrange the
remaining n-1 books. This is true because the next book on the
shelf, under the problem conditions, has to be a M book. Thus,
with a S book first, we are sure of the first two books shelved.
Now there remain F(n-2) ways to arrange the remaining n-2
books.
Because the two cases are distinct, we have
F(n)=F(n-1)+F(n-2).
?
Recursion (점화식) :
The relationship described by F(n)=F(n-1)+F(n-2) is called a
recursion relationship(점화관계), a relationship in which a
new element is described by referring to one or more known
elements. We have seen many recursion relationships in our
study of mathematics, although that fact may not have been
directly stated at the time. Here are some examples of
recursion relationships. With each, some specific elements in
the relationship are shown as well as a corresponding explicit
way to describe each relationship.
다음의 표는 몇 가지 점화식과 그 일반항을 나타낸다.
Recursion Relation |
Sample Elements |
Explicit Form for the
Relation |
C(N)=N*C(N-1), C(0)=1 |
C(1)=1*C(0)=1
C(2)=2*C(1)=2
C(3)=3*C(2)=6 |
N! |
a(n)=a(n-1)+4, a(1)=6 |
a(2)=a(1)+4=10
a(3)=a(2)+4=14 |
a(n)=4n+2 |
b(m)=2*b(m-1), b(1)=3 |
b(2)=2*b(1)=6
b(3)=2*b(2)=12
b(4)=2*b(3)=24 |
b(m)=3*2^(m-1) |
t(n)=t(n-1)+n, t(1)=1 |
t(2)=t(1)+2=3
t(3)=t(2)+3=6 |
t(n)=(n*(n-1))/2 |
Throughout this lecture,
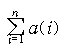 . .
The handout from last time asked you to explore some
examples of determining the number of ways to complete
specific tasks given certain restrictions. For two of the three
situations we have already developed machinery to solve the
problem. The third situation, involving Sandy Softknuckle's
arrangements of napkins, extends our work. We will use Sandy
Softknuckle's setting to illustrate the three situations.
Sandy Softknuckle suffers from a mild case of
obsessive-compulsive disorder. Sandy is
particularly fascinated with ways to arrange
dinner napkins for formal parties. Assuming
Sandy has an unlimited supply of green, white,
and red napkins, how many ways can Sandy
create a set of 20 napkins if:
a) it is okay to have no napkins of a particular
color?
b) there must be at least one napkin of each
color?
c) there must be more than 3 of each color
napkin?
The two situations previously encountered:
(a) The number of solutions to the equation Sigma(i,1,n;a(i))=K
solved over the nonnegative integers is C(K+n-1,n-1). Here, we
have C(20+3-1,3-1)=C(22,2).
(b) The number of solutions to the equation Sigma(i,1,n;a(i))=K
solved over the positive integers is C(K-1,n-1). Here, we have
C(20-1,3-1)=C(19,2).
(c) For the third situation, we introduce a new set of variables to
help us reduce the problem to one we have already solved.
Let us write the equation g + w + r = 20 to represent the need to
have 20 napkins of three colors. The problem situation requires
that g > 3, w > 3, and r > 3. Then g-3 > 0, w-3 > 0, and r-3 > 0.
Use a, b, and c to represent the left side of each of these
inequalities: We have a = g-3 > 0, b = w-3 > 0, and c = r-3 > 0.
This gives us a + b + c = (g-3) + (w-3) + (r-3) = (g + w + r) - 9.
Because we must have g + w + r = 20, we get a + b + c = (g + w
+ r) - 9 = 11.
Thus, we are left with the condition that a + b + c = 11, where
each of a, b, and c must be a positive integer. We know how to
determine the number of solutions to this equation (see part (b)
above). It is just C(11-1,3-1) = C(10,2).
We could have generated the same solution using a slightly
different argument, as follows:
The problem situation requires that g >= 4, w >= 4, and r >= 4.
Then g-4 >= 0, w-4 >= 0, and r-4 >= 0. Use x, y, and z to
represent the left side of each of these inequalities: We have x
= g-4 >= 0, y = w-4 >= 0, and z = r-4 >= 0.
This gives us x + y + z = (g-4) + (w-4) + (r-4) = (g + w + r) - 12.
Because we must have g + w + r = 20, we get x + y + z = (g + w
+ r) - 12 = 8.
Thus, we are left with the condition that x + y + z = 8, where each
of x, y, and z must be a nonnegative integer. We know how to
determine the number of solutions to this equation (see part (a)
above). It is just C(8 + 3 -1,3-1) = C(10,2).
We see that either approach generates the same solution:
C(10,2).
Problem 1. Try to generalize the previous results.
|
이제 위의 생각해볼 문제에서 연구했던 triangulation에
관하여 조금 더 생각하여 봅시다.
6.Eulers's Polygon -Triangulation Problem. It was Euler who
first discovered the Catalan numbers through a
combinatiorial problem in plane geometry which be posed to
Christian Goldbach in 1751.
In how many ways can a convex polygon of n sides be
divided into triangles by drawing diagonals that do not
intersect?
Find an explicit fomula for the number Dn of different
triangulations.
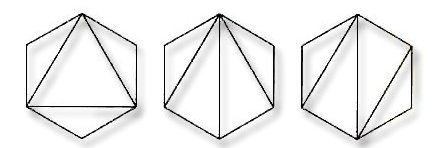
FIGURE 2.
a. Calculate D3 , D4, D5, D6 .
b. Show that no matter how the n-gon is triangulated,
the number of diagonals is always n-3 and the number
of triangles is n-2.
c Define D2 =1 and show that for n≥3
Dn = D2Dn-1+ D3Dn-2+ D4Dn-3 +... +Dn-1D2.
d.Conclude that {Dn} is the sequence of Catalan
numbers, and hence that
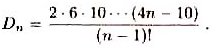
|