표준적 증명방법으로 수학적 귀납법을 사용하는

문제와 유한차분에 관하여 학습하도록 한다.

수학적 귀납법과 유한차분

 

먼저  표준적 증명방법으로 수학적 귀납법을 사용하는

문제와 유한차분법에 관하여 알아봅시다.

  제 6주 강의록은 영문으로 작성되었습니다.  국문강의록 보다 읽기가 조금 어렵기 때문에 여러분들은 천천히 읽고 학습하기 바랍니다.

   Throughout this lecture,  

we denote   Sigma(i,1,n;a(i))  by

                   .

         Using Induction

     We briefly introduced the use of summation and product notation as means for concisely representing mathematical expressions. Determine the value of each of the following expressions:

• sigma[i,1,4;(2i-3)]=8
• sigma(j,0,6;j^2)=91
• sigma(p,1,n;p)=[n(n+1)]/2
• Pi(n,3,6;n)=360
• Pi(w,4,7;w-2)120
• Pi(a,1,n;a)=n!
• Pi(k,1,6n-7;k-1)=0

Proof by Induction

We illustrate the process of proof by induction to show that

(I) sigma(i,1,n;i)=[n(n+1)]/2.

+Process

Step 1: Verify that the desired result holds for n=1.

Here, when 1 is substituted for n in both the left and right side expressions in (I) above, the result is 1. Specifically, sigma(i,1,1;i)=1 and [1(1+1)]/2=1. This completes step 1.

Step 2: Assume that the desired result holds for n=k.

In our example, this means that we assume the sum of the first k positive integers is [k(k+1)]/2. It will be helpful to show this as

(II) 1+2+...+k=[k(k+1)]/2.

Step 2 is complete.

Step 3: Use the assumption from step 2 to show that the result holds for n=(k+1).

That is, we want to show that sigma(i,1,(k+1);i)=[(k+1)(k+2)]/2. In other words, show that assuming the result for n=k implies the result for n=(k+1).

Here, we build on the equation presented in (II): If 1+2+...+k=[k(k+1)]/2, adding (k+1) to each side assures us that 1+2+...+k+(k+1)={[k(k+1)]/2}+(k+1). The left side is just the expansion of the expression sigma(i,1,(k+1);i), that is, the sum of the first (k+1) positive integers.

We are left to show that the right side is equivalent to [(k+1)(k+2)]/2, what our formula tells us is the correct sum. Rewrite the right side {[k(k+1)]/2}+(k+1) with a common denominator: {[k(k+1)]/2}+[2(k+1)]/2. Now add numerators and express over the common denominator: [k(k+1)+2(k+1)]/2. In the numerator, (k+1) is common to both terms, so we can factor the numerator into its equivalent form [(k+1)(k+2)]/2.

This last expression is just the result we sought.

Step 4: Summarize the results of your work.

We have shown by induction that the sum of the first n positive integers can be represented by the expression [n(n+1)]/2.

As an equation, we have sigma(i,1,n;i)=[n(n+1)]/2. This has practical application any time we seek sums of consecutive positive integers. For example, we can now use the result to conclude that sigma(i,1,10;i)=10(11)/2=55. We can also use the result to show that, for example, sigma(i,4,8;i)=sigma(i,1,8;i)-sigma(i,1,3;i).

+Summary

The induction process relies on a domino effect. If we can show that a result is true from the kth to the (k+1)th case, and we can show it indeed is true for the first case (k=1), we can string together a chain of conclusions: Truth for k=1 implies truth for k=2, truth for k=2 implies truth for k=3, and so on. Pushing the first domino causes all of the remaining dominoes to fall in succession.

 

문제 1.   Here are practice problems to reinforce the induction process. Show that sigma(k,1,n;2k)=(n^2+n). Show that sigma[j,1,n;2^(j-1)]=(2^n-1). Show that the sum of the first n odd positive integers is n^2. Explore patterns in the sums 1/(1x2), [1/(1x2)]+[1/(2x3)], [1/(1x2)]+[1/(2x3)]+[1/(3x4)], and so on. Use proof by induction to justify your conjecture.

Recursion Relationships

Last time, we introduced the idea of a recursion relationship in the context of Fibonacci's Sequence. Tonight we review the idea of recursion by first developing a recursion relationship for a pattern in Pascal's Triangle.

Let's write a recursion relationship for the sum of the elements in the first column of the triangle. That is, find a recursion relation to represent the values 1, 3, 6, 10, and so on.

We first identify the initial conditions. Here, we can use S(1)=1 to indicate that the first sum is 1. Now, how can we use that term to get to the next one?

We want S(2) to be represented in terms of S(1), if possible. We note that S(2) = S(1) + 2 = 3. We also note that the Sum #2 is generated by adding 2 to Sum #1.

In general, the nth sum, S(n), is found by adding n to the (n-1)th sum. That is, S(n) = S(n -1) + n. This is a recursion relationship to describe the sums of the elements in the first column of Pascal's Triangle.

Try to determine recursion relationships for each of the following sequences or situations.

• 5, 10, 15, 20, 25, . . .
• 2, 4, 8, 16, . . .
• 10, 7, 4, 1, . . .
• 80, 20, 5, . . .
• the number of people that can be seated at k square tables lined up adjacent to one another, under the condition that one person sits at each available side of a table.

Now try to determine an explicit representation for each of the sequences or situations above.

Finite Differences (유한차분)

We begin our discussion of finite differences by examining the third column in Pascal's Triangle: 1, 4, 10, 20, 35, 56, . . . . Suppose we seek an explicit representation for this sequence. One way to do that is simply to use combination notation: C(n,3) for n at least 3. This simplifies to [n(n-1)(n-2)]/6. There we have an explicit representation.

Another way to search for an explicit representation is to use the method of finite differences. Let us illustrate the method.

To use the method of finite differences, generate a table that shows, in each row, the arithmetic difference between the two elements just above it in the previous row, where the first row contains the original sequence for which you seek an explicit representation.

Here are the first few rows for the sequence we grabbed from Pascal's Triangle:

Notice that the third-differences row is constant (i.e., all 1s). This is the signal we look for in an application of finite differences. If and when we reach a difference row that contains one value, we can write an explicit representation for the relationship. In fact, we can be more specific and say that the relationship is a polynomial whose order is equal to the row number of the initial row in which the constant difference occurs. In our example, because the constant difference first occurred in the third row of differences, a third-degree, or cubic, polynomial can be found to represent the relationship.

The next question: how do we find that polynomial representation?

We return to a difference table, but replace the elements in the first row with more general terms. In our example, if the elements in the row of original values are generated from a cubic polynomial, they all are of the form an^3+bn^2+cn+d. We compute these values for n=1,2,3 and so on, to represent the first value in the row, the second value in the row, and so on.

When n=1, an^3+bn^2+cn+d=a+b+c+d. When n=2, an^3+bn^2+cn+d=8a+4b+2c+d. Likewise, we get 27a+9b+3c+d when n=3, 64a+16b+4c+d when n=4, 125a+25b+5c+d when n=5, and 216a+36b+6c+d when n=6.

Here's the difference table with these general elements in the original row, followed by the subsequent differences:

As expected, we see a constant difference in the third row of differences. How does that help us? Compare this to the last row of our first table, where the constant differences were all 1. Setting the two rows equal to each other, we have 6a=1, or a = 1/6. This shows us that in the cubic polynomial we seek, of the form an^3+bn^2+cn+d, we know that a=1/6.

Continuing back up the tables, and knowing that a=1/6, we can write the equation 12(1/6)+2b=3, or b=1/2. Equating the first row of differences in each table, and knowing that a=1/6 and b=1/2, we can write the equation 7(1/6)+3(1/2)+c=3, showing that c=1/3. We can then determine from a+b+c+d=1 and a=1/6, b=1/2, c=1/3 that d=0.

Putting all this together into the general cubic an^3+bn^2+cn+d, we determine that 1/6n^3+1/2n^2+1/3n, or, equivalently, (1/6)(n^3+3n^2+2n)=(1/6)(n)(n+1)(n+2). Now test this. For n=1, we get 1; for n-2, the expression simplifies to4; when n=3, we get 10. These are just the first three values of the original sequence, as expected.

Here are some related problems for you to complete:

1. Create the difference tables for the general linear polynomial ax+b and the general quadratic polynomial ax^2+bx+c.
2. Create a difference table for the sequence 12, 28, 50, 78, 112, 152, . . . . What type of relationship is represented? how do you know?
3. Calculate the first several terms (n=1,2,3,...) of the sequence represented by the polynomial 2n^3+2n^2+n. In a difference table generated from this sequence, in what row will the differences first appear constant? What is that constant difference?

Here are the first four rows of a triangular array of numbers:

Use the method of constant differences to determine an explicit representation for the row sums.

      표준적 증명방법으로 수학적 귀납법을 사용하는

문제와 유한차분에 관하여 학습하도록 한다.

 

If  ten people check their hats, and drunken hat-checked

girl returns the hats randomly to the people,  what is the

probability that no one gets the right hat ?

  본 강의에서는 앞에서 학습한 포함 배제의 원리에 대하여

 다시 알아보고 그 응용에 대하여 학습한다.

 The Inclusion-Exclusion Principle and        Rearrangements,   Revisited

본 강의에서는 앞에서 학습한 포함 배제의 원리에 대하여

다시 알아보기로 한다.

  제 6주 강의록은 영문으로 작성되었습니다.

 국문강의록 보다 읽기가 조금 어렵기 때문에

여러분들은 천천히 읽고 학습하기 바랍니다.

The Inclusion-Exclusion Principle (포함배제의 원리)

Our fundamental goal is to efficiently determine the number of elements in a set that possess none of a specified list of properties or characteristics. We begin with several examples to generate patterns that will lead to a generalization, extension, and application.

 

EXAMPLE 1: Suppose there are 10 spectators at a ball game and 4 are wearing caps. How many spectators are not wearing caps?

Straightforward subtraction yields the result: 10 - 4 = 6. There are 6 spectators not wearing caps. Let us introduce mathematical notation that will, eventually, be helpful in expressing a generalization of this result.

If we use T to represent all spectators and C to represent the property "wearing a cap," we can apply conventional mathematics notation to represent the number of items or elements having the property: |T| = 10 and |C| = 4. We typically use a slash over the top of the letter to represent the complement of the property. [For this web page, we will use a tilda (~) to represent the complement.] So ~C is the property "not wearing a cap." This gives us |~C| = |T| - |C| = 10 - 4 = 6.

 

EXAMPLE 2: In the set S = {1,2,3,...,100}, how many elements are not divisible by 3?

Let's use D to represent the set of values divisible by 3. From the previous problem, it seems we need |~D| = |S| - |D|. We know |S| = 100. The set D = {3,6,9,...,99} and it has 33 elements. We get |~D| = 100-33 = 67. Therefore, 67 elements of S are not divisible by 3.

 

EXAMPLE 3: Among 10 students, 5 study mathematics, 6 study science, and 2 study both. How many of these students study neither mathematics nor science?

For this problem, we first refer to a Venn diagram, a visual tool we could have employed in the first two examples as well. In the figure here we represent each property with a circle, and the portion on the circles that overlap, or intersect, represents elements with both the properties. We use T to represent the entire group of students, M to represent the property "study mathematics" and S to represent the property "study science."

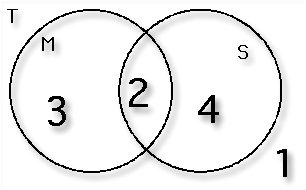
We know there are 2 people who study both mathematics and science, so we place a 2 at the intersection of the two properties (circles). We must then have 3 who study mathematics but not science (because 5 in all study mathematics), and 4 who study science but not mathematics (because 6 in all study science). This accounts for 9 people, so the remaining 1 person must study neither mathematics nor science.

This is a relatively straightforward determination, especially with the aid of the Venn diagram. How do our calculations compare to those made in the first two examples? We have |T| = 10, |M| = 5, |S| = 6, and |M^S| = 2. [Note that on this web page we use ^ to represent the intersection of two sets. Normally this is an inverted U.]

But |~M^~S| is not equal to |T| - (|M| + |S|), a pattern we might have tried based on the first two examples. Why is this insufficient? Look back at the Venn diagram. When we subtract |M| and |S| from |T|, we are twice subtracting the number of elements in the intersection of the two sets. That is the value 2 here, or in general, |M^S|. To compensate for the "over" subtraction, we add back |M^S|, as follows: |~M^~S| = |T| - (|M| + S|) + |M^S|.

 

EXAMPLE 4: Among 18 students in a room, 7 study mathematics, 10 study science, and 10 study computer programming. Also, 3 study mathematics and science, 4 study mathematics and computer programming, and 5 study science and computer programming. We know that 1 student studies all three subjects. How many of these students study none of the three subjects?

We are looking for |~M^~S^~C|, where M, S, and C represent belowing to the group that studies each of the three subjects mathematics, science, and computer programming, respectively. Consider the Venn diagram below. Can you justify each entry in the diagram, starting from knowing that |M^S^C| = 1? How many students study none of the three subjects?

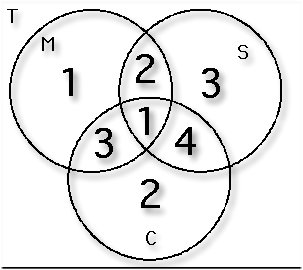
Trying to use and generalize the patterns we've established above, consider |M| + |S| + |C|. What values are "over counted" here? When we subtract |M ^ S| + |M ^ C| + |S ^ C| from |M| + |S| + |C| to compensate, what values are "over" subtracted? What can be done to compensate for this?

 

EXAMPLE 5: Extend the patterns generated thus far in order to solve the following problem. Draw a Venn diagram if desired:   In  a mathematics department of 40, faculty are members represent four different professional organizations: NCTM (N), MAA (M), AMS (A), and SSMA (S). We know that 21 are members of NCTM, 26 are MAA members, 19 belong to AMS, and 17 are in SSMA. In addition, we know that 15 are in both NCTM and MAA, 6 are in NCTM and AMA, 9 are in NCTM and SSMA, 14 and in MAA and AMS, 10 are in MAA and SSMA, and 11 are in AMS and SSMA. We also know that 6 are in NCTM, MAA, and AMS, 5 are in NCTM, MAA, and SSMA, 4 are in NCTM, AMS, and SSMA, and 9 are in MAA, AMS, and SSMA. finally, 4 people belong to all four organizations. How many faculty members belong to none of these organizations?

 

EXAMPLE 6: Extend the patterns developed thus far to write a general formula for determining the number of items in a set that possess none of  k properties maintained by the set. This is the Inclusion-Exclusion Principle.

 

EXAMPLE 7: Manipulate the results you generated in Example 6 to determine the number of items in a set that possess at least one of the k properties maintained by the set.

 

EXAMPLE 8: Now apply the Inclusion-Exclusion Principle to the problem of derangements:

In an apartment complex with k mailboxes, how many ways can a mail carrier distribute k letters, one addressed to each letter box, such that no letter is placed in the correct box? Each of these is called a derangement.

 Recall that our goal was to efficiently determine the number of elements in a set that possess none of a specified list of properties or characteristics. We began with several examples to generate patterns that led to a generalization. Today we review the generalization, suggest an extension, and use the I-E P to solve a problem.

The notation we introduced last time included the use of a capital letter (for example, C) to represent a property under consideration. To represent the number of items or elements having the property, we surrounded the capital letter with vertical slashes (for exampe, |C|). We used a slash over the top of the letter to represent the complement of the property. [For this web page, we use a tilda (~) to represent the complement.] So ~C is the property "not property C."

Through consideration of special cases and the illustrative use of Venn diagrams, we developed the Inclusion-Exclusion Principle to be

|~X(1) ^ ~X(2) ^ . . . ^ ~X(n)| = |S| - sigma(i,i,n;|X(i)|) + sigma[j,1,n; sigma(i,j+1,n;|X(j) ^ X(i)|)] - . . . + (-1)^n|X(1) ^ X(2) ^ . . . X(n)|.

where S represents the entire set of items, each of which possesses from none to all of the properties X(i), i = 1,2,...,n.

If we remove from S all items possessing none of the specified properties, we are left with items that possess at least one of the properties. This may be a useful corollary for application. Symbolically we have

|X(1) U X(2) U . . . U X(n)| = |S| - |~X(1) + ~X(2) + . . . + ~X(n)| = sigma(i,i,n;|X(i)|) - sigma[j,1,n; sigma(i,j+1,n;|X(j) ^ X(i)|)] + . . . + (-1)^(n+1)|X(1) ^ X(2) ^ . . . X(n)|.

In the next section we apply the I-E P to a condition called a derangement, requiring us to count the ways that "no properties hold."

Derangements

Here is a context representing the need to determine how many derangements there are for a specified number of objects:

In an apartment complex with k mailboxes, how many ways can a mail carrier distribute k letters, one addressed to each letter box, such that no letter is placed in the correct box? Each such distribution scheme is called a derangement.

We begin by determining the number of derangements for specific values of k, seeking to identify patterns in our calculations that may lead to a conjecture for a general representation for the number of derangements of n items.

Let us refer to a letter by a number and to a mailbox by a number. Our task is to determine the number of ways to pair letters and boxes so that no letter numbers match box numbers. If k = 1, there are no ways to derange the letter, for there is one letter to place in one box. If k = 2, we may place letter #2 in box #1 and letter #1 in box #2, that being the only derangement.

When we have three letters, there are 3! = 6 total ways to distribute them. We now write the letter numbers in the order they are delivered, such as 1 3 2, indicating letter #1 is delivered to box #1, letter #3 is delivered to box #2, and letter #2 is delivered to box #3. The 6 possible distributions for 3 letters are

1 2 3     1 3 2

2 1 3     2 3 1

3 1 2     3 2 1

The schemes 2 3 1 and 3 1 2 are the only derangements of three letters.

Summarizing our results thus far, using D(n) to represent the number of derangements of n letters, we have D(1) = 0, D(2) = 1, and D(3) = 2. Any guesses on D(4)? Let's find out what it is.

We know there are 4! = 24 ways to distribute the 4 letters. Rather than list the 24 cases, let us consider how the I-E P may help us. We seek the number of ways to place the numbers in the set {1,2,3,4} in line such that no value occurs in its natural position. Let X(1) represent the property that 1 occurs in its natural position when 1,2,3,4 are permuted. Then |X(1)| = (1)*3!. The 1 represents the 1 way to place the 1 in its natural position and the 3! shows the number of ways to permute the remaining 3 values. Note that we are not considering whether any of 2,3,4 wind up in their respective natural positions. We could argue similarly that |X(2)| = |X(3)| = |X(4)|. Therefore, there are 4*3! ways for a value to occur in its natural position.

What about |X(1) ^ X(2)|? Again there is 1 way to place 1,2 in their natural order, and then 2! ways to place the remaining values. This will be true for any pair of values we wish to restrict to their natural positions. How many pairs are there? This is just C(4,2) = 6. Therefore, there are C(4,2)*2! ways for two values to simultaneously occur in their natural positions.

And for |X(1) ^ X(2) ^ X(3)|? Again there is 1 way to place 1,2,3 in their natural order, and then 1! way to place the remaining value. This will be true for any set of three values we wish to restrict to their natural positions. How many 3-element sets are there? This is just C(4,3) = 4. Therefore, there are C(4,3)*1! ways for three values to simultaneously occur in their natural positions.

Finally, |X(1) ^ X(2) ^ X(3) ^ X(4)| = 1, for there is only one way for all 4 values to be in their natural positions.

Now apply the I-E P:

|~X(1) ^ ~X(2) ^ ~X(3) ^ X(4)| = 4! - 4(3!) + 6(2!) - 4(1!) + 1 = 9. In words, using the I-E P, we are suggesting that to determine the number of derangements of the values 1,2,3,4, first calculate the number of permutations of those values (4!), subtract the number of ways to keep at least one element in its natural position, add back the number of ways to keep at least two values in their natural positions, subtract the number of ways to keep at least three values in their natural positions, and finally add back the number of ways to keep all values in their natural positions.

We can rewrite the right side of the above equation to better express the general result:

D(4) = |~X(1) ^ ~X(2) ^ ~X(3) ^ X(4)| = 4! - 4(3!) + 6(2!) - 4(1!) + 1
=C(4,0)*4! - C(4,1)*3! + C(4,2)*2! - C(4,3)*1! + C(4,4)*0!
=[4!/(0!4!)]*4! - [4!/(1!3!)]*3! + [4!/(2!2!)]*2! - [4!/(3!1!)]*1! + [4!/(4!0!)]*0!
=4!/0! - 4!/1! + 4!/2! - 4!/3! + 4!/4!
=4![1/0! - 1/1! + 1/2! - 1/3! + 1/4!]
=4![1 - 1/1! + 1/2! - 1/3! + 1/4!]

If we begin with n objects rather than 4, we can argue in a similar way that

D(n) = n![1 - 1/1! + 1/2! - 1/3! + . . . (-1)^n*1/n!]

determines the number of derangements of n items.

Derangement에 관하여는  제 4주  4 강의를

참고하기 바랍니다.

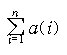앞에서 학습한 포함 배제의 원리에 대하여

       다시 알아보고 그 응용을 학습하였다.