황금비와 Fibonacci 수
이제 Fibonacci수열의 기하적 응용 중의 한 가지를
학습하도록 합시다.
한 선분을 두 부분으로 나누되
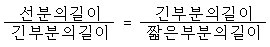
가 되도록 나누는 것을 황금분할 (golden
section)이라 하고 그 비를 황금비(golden
ratio)라고 한다.
주어진 선분의 길이와 긴 부분의 길이를 각각 l, a
라 하고 황금비를
g 라고 하면,

황금비는 예술적으로 가장 이상적인 비율이라고 여겨
지고 있다.
황금비 g는 흔히 보는 책의 가로의 길이에 대한
세로의
길이의 비의 값과 같고, 또 한변의 길이가 1인
정5각형의
대각선의 길이와도 같다.
정의 1. 다음과 같이 귀납적으로 정의된 정수
Fn을 Fibonacci수 라고 한다.
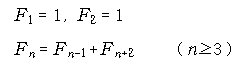
또, 수열 { Fn}을 Fibonacci 수열이라고 한다.
|
따라서 Fibonacci수열의 처음 몇 항을 써보면 다음과 같다.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ....
Fibonacci수열이 갖는 다음과 같은 성질을
알아보도록 한다.
정리1. Fibonacci수 Fn 에 대하여 다음이
성립한다.
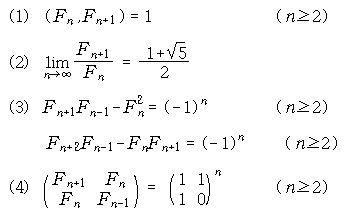
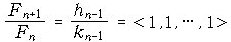
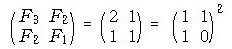

|
수학적 귀납법을 이용하여 다음 등식이 성립함을
증명할 수 있다.

임의의 양의 정수는 2의 거듭제곱
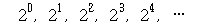
의 합으로 나타낼 수 있다. 예를 들면,
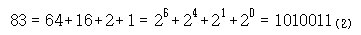
마찬가지로, 임의의 양의 정수는 Fibonacci수들이 합으로
나타낼 수 있다. 이 때,

전자계산기를 사용하여 동일한 양을 여러 번 더하는
경우에, 흔히 이와
같은 Fibonacci분할법을 이용하여 계산한다.
|