분할 (partition)
앞에서 학습한 선형 Diophantine 방정식을 다시 생각하여
봅시다.
x + y + z = 5를 만족하는 자연수해 중에서 (3,1,1)과
(1,3,1)은 서로 다른 해를 의미한다. 그렇지만 순서를 무시하고
단순히 구성성분으로만 이해한다면 두 해 모두 1, 1, 3 이라는
구성성분 만을 갖고 이는 자연수 5 의 분할 (partition)이
된다.
정의. 자연수 n에 대한 (unordered) partition (분할)이란
원소의 총합이 n이 되는 자연수들의 집합을 의미한다.
|
예를 들면, 5의 분할은
5 ; 4+1; 3+2; 3+1+1; 2+2+1; 2+1+1+1; 1+1+1+1+1
등 모두 7 가지이다.
자연수 n에 대한 unordered partition의 개수를 P(n) 이라고
표시하기로 합시다. 그러면,
임을 알 수 있다.
일반적으로 커다란 수 n에 대한 P(n)을 알기는 무척
어렵다. 물론, 일반적인 n에 관한 P(n)의 식은 알려져 있지
않다.
이제 분할에 대한 간단한 성질을 알아보도록 합시다.
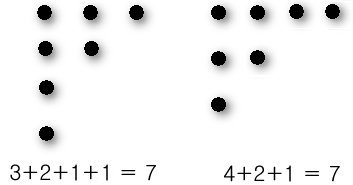
위의 그림에서와 같이 행과 열이 서로 바뀐 모양의 분할을
공액 (conjugate)인 분할이라고 한다.
위의 그림은 7 에 대한 공액인 분할이다.
이제 분할의 성질을 알아보기 위하여 기하적 분할의 모양인
Ferrer의 diagram을 이용하여 다음 그림을 생각해 봅시다.
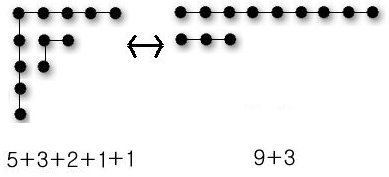
위 그림에서 12의 분할 중에서 두 분할
5+3+2+1+1 과 9+3
의 Ferrer의 diagram이라고 하며, 마찬가지로
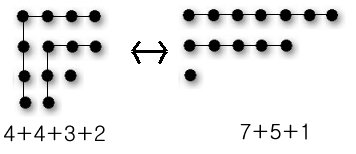
13의 분할 중에서 두 분할
4+4+3+2 와 7+5+1
의 Ferrer의 diagram이라고 부른다.
이제 위의 Ferrer의 diagram을 이용하면, 다음과 같은
정리를 얻을 수 있다.
정리 1. 자연수 n을 m부분으로 나눈 분할의 개수는
분할의 최대 구성성분의 크기가 m인 분할의 수와 같다.
|
위 정리는 다음 그림과 같이 이해할 수 있다.
예를 들면, 5를 세 부분으로 나눈다면,
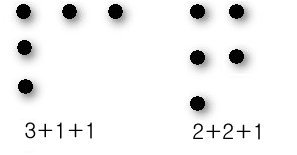
이 되는데, 두 분할에서 1열을 한 수로 이해한다면,
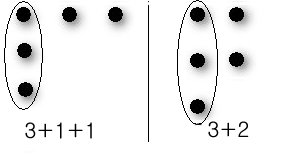
가 되어 위 정리가 옳음을 확인할 수 있다. ?
문제 2. 자연수 7을 세 부분으로 나눈 분할의 개수를 구하고,
구성성분 중 가장 큰 수는 얼마인가 구하시오.
|
다음 정리는 Ferrer의 diagram을 이용하여 분할의 개수를
구하는 방법을 나타낸다.
정리 2. 자연수 n의 분할 중에서 모든 구성성분이
홀수이고서로 다른 것의 개수는 self conjugate (즉,
conjugate가자기 자신과 같은 분할)인 분할의 Ferrer
diagram으로 구할 수 있다.
|
증명. 우리는 다음 그림에서와 같이 두 종류의 분할 사이에
Ferrer diagram이 일대일 대응을 이루고 있음을 알 수 있다.

 ? ?
문제 3. 자연수 15 의 분할 중에서 구성성분이 홀수이고 서로
다른 것의 개수는 모두 몇 개인가 구하시오. 또,이들의 Ferrer
diagram을 이용하여 self conjugate인 분할도 구하시오.
|
자연수 n의 분할 중에서, n 이하인 모든 자연수 k는 n의 분할의
구성성분으로 항상 유일하게 표시할 수 밖에없을 경우, 이러한
분할을 우리는 완전(perfect)하다고 부른다.
즉, 1+1+1+ ... +1 과 같은 분할은 perfect한 분할이다.
또 7의 perfect한 분할은
4+1+1+1 ; 4+2+1 ; 2+2+2+1 ; 1+1+1+1+1+1+1
등이 있다. 그러나 분할
5+1+1
은 perfect한 분할이 아니다. 예를 들면, 3은
1+1+1 또는 2+1
로 표시할 수 있기에 유일한 표현이 되지 못한다.
우리는 완전분할에 대한 일반식은 쓸 수 없지만 다음과 같은
정리는
매우 유용한 식이다.
정리 3. 자연수 n에 대한 perfect partition의 개수는
자연수 n+1에 대한 인수분해 중에서 구성성분이 2 이상이고
순서를 고려한 인수분해의 종류의 개수와 일치한다.
|
증명. n은 1 이상이므로 1은 모든 perfect partition의 원소임이
분명하다. 먼저 완전 분할에서 1이 m1 - 1 개 있다고 하자. 그러면,
m1이 m2 - 1 개 있다고 하면 우리는 m1 m2 보다 작은 모든 수는
유일하게 표시할 수 있다. 마찬가지로 다음 구성원소는 m1 m2 이고
이것이 m3 - 1 개 있다고 가정하고 위와 같은 방법을 반복하면, 우리는
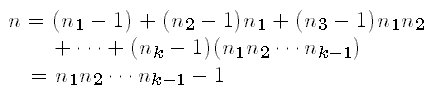
임을 알 수 있다. 따라서,
n+1 = m1 m2 ... mk 이고, 모든 i 에 대하여 mi 는 2 이상이다.
그러면, 분명히 인수분해
m1 m2 ... mk
는 n 의 완전분할이 된다. ?
풀이. 12 = 11 + 1 의 ordered factorization 과 대응하는 11의
완전분할을 모두 쓰면 다음과 같다.
6 x 2 ------------- 1+1+1+1+1+6
4 x 3 ------------- 1+1+1+4+4
3 x 4 ------------- 1+1+3+3+3
2 x 6 ------------- 1+2+2+2+2+2
3 x 2 x 2 ---------- 1+1+3+6
2 x 3 x 2 ---------- 1+2+2+6
2 x 2 x 3 ---------- 1+2+4+4 ?
문제 4. 다음 분할의 conjugate 분할을 모두 구하시오.
(1) 7 = 4+1+1+1
(2) 9 = 6+2+1
|
문제 5. 9의 모든 perfect partition을 구하시오.
|
문제 6. n의 perfect partition의 원소의 개수는 n+1의
인수가 됨을 증명하시오.
|
문제 7. n의 perfect partition이 오직 1+1+...+1 뿐인
경우
n은 어떤 조건을 만족하는 자연수이어야 하는가 구하시오.
|
|