포함배제의 원리
광범위한 응용을 갖는 세기의 방법에 대하여 알아봅시다.
임의의 집합 S 에 대하여 n(S) 를 집합 S 의 원소의 개수를 나타낸다고
하자. 이 때, n 개의 집합 S1,S2, ..., Sn 이 주어졌을 때,
n ( S1 ∪ S2 ∪ ... ∪ Sn )
을 구하여 봅시다.
먼저 얼마나 많은 원소들이 겹쳐 있는가를 알아보아야 된다. 만일 집합이
S1, S2 두 개인 경우에는
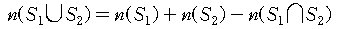
임을 쉽게 알 수 있다. 따라서 세 집합 S1,S2,S3 에 대하여
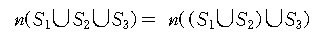
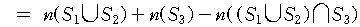
집합의 연산법칙(De Morgan의 정리)에 의하여
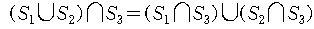
이므로,
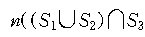 ) )
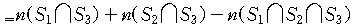
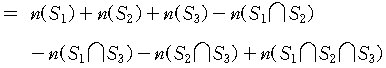
위의 식을 일반화하면 다음의 포함배제의 원리
(the principle of inclusion and exclusion)를 얻을 수
있다.
|
n(S)는 집합 S의 원소의 개수를 나타낼 때, S1,S2,... Sn이
유한집합이면 다음의 식을 얻을 수 있다.
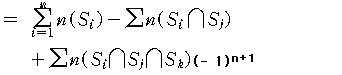
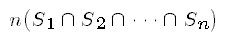 |
증명은 다음을 참고하여 수학적 귀납법을 사용하여 각자 써 보시오.
아래에서 A'은 A의 여집합을 나타낸다.
The principle of Inclusion and Exclusion :
N(α'1 α'2 ... α'n-1α'n) = N - N(α1) - N(α2)- ... - N(αn)
+N(α1α2) +N(α1α3) + ... + N(αn-1αn)
-N(α1α2α3) -N(α1α2α4) - ... - N(αn-2αn-1αn)
+ ... ... ...
+(-1)n N(α1α2 ...αn-1αn). (3.1)
Proof. The proof is by induction on the number of
properties, that is , on the number n. if n=1 the formula
is N(α'1 )=N-N(α1 ) , which is obvioulsy true.
Suppose (3.1) is true for n-1 properties. Using the
formula on the objects that have a property α1 . we
obtain.
N(α'1α'2 ...α'n-1αn)=
N(αn)-N(α1αn)-N(α2αn)-...-N(αN-1αn)+
N(α1α2αn)+N(α1α3αn)+...+N(αn-2αn-1αn)+
... ... ... ...
+(-1)n-2 N(α1α2 ...αn-2αn)+...
+(-1)n-2 N(α2α3 ...αn-1αn)+
(-1)n-1 N(α1α2 ...αn-1αn). (3.2)
We also have
N(α'1α'2 ...α'n-1) = N - N(α1)-N(α2)-...-N(αn-1)
+N(α1α2)+N(α1α3)+...+N(αn-1αn-2)+
...+(-1)n-1 N(α1α2α3 ...αn-1). (3.3)
Subtracting (3.2) from (3.3), we get the formula (3.1) if we
note that
N(α'1α'2 ...α'n-1) - N(α'1α'2 ...α'n-1αn)
Thus assuming the principle of inclusion and exclusion for
n-1, we have derived if for n. ?
예제 1. 54명의 회원을 가진 Sports club이 있다. 회원
중 34명은 tennis, 22명은 golf, 10명은 tennis와
golf를 한다. 또, 11명은 handball, 6명은 handball과
tennis, 4명은 handball과 golf, 2명은세 가지 운동을
모두 한다. 이 때, 아무 운동도 하지 않는 사람은 몇
사람인가 구하시오.
|
풀이 . 위의 각 조건을 다음과 같은 벤 다이어그램에 나타내 봅시다.
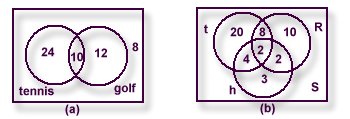
따라서 위 벤다이어그램에서 확인할 수 있듯이, 어떤 운동도 하지 않는
사람은 5명이다. 또,
n(S) : Sports club 회원 수
n(T) : tennis 하는 회원 수
n(H) : handball 하는 회원 수
n(G) : golf 하는 회원 수
라 두면, 우리가 구하는 수는
n(S) - [n(T)+ n(H) +n(G)- n(T∩H)
- n(T∩G) -n(H∩G)+ n(T∩H∩G)]
이고, 따라서
54 - 34 - 22 - 11 + 10 + 6 + 4 - 2 = 5
이다. ?
문제 2. 0부터 999까지의 수 중에서 5 또는 7로
나누어지는 수의 개수는 모두 몇 개인가?
또, 5 또는 7로 나누어지지 않는 수의 개수는 모두
몇 개인가?
|
정수론에 나오는 중요한 함수로 Euler Φ-함수가 있다.
Φ(n) 은 n 보다 작은 자연수 중에서 n 과 서로 소(relative prime)인
수의 개수를 나타낸다. 그리고 Φ(1) = 1 이라고 두자.
그러면 Φ(36) = 12 이다. 실제로 36 보다 작은 수 중에서 36과
서로 소인 수는
1 5 7 11 13 17 19 23 25 29 31 35
등 모두 12개 이다.
만일 n 이 서로 다른 소수(prime number) 를 인수로 갖는다면,
우리는 포함배제의 원리에 의하여
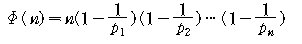
을 증명할 수 있다. (증명은 정수론 책을 참고하시오.)
예를 들면, 36은 소인수로서 2, 3 이 있으므로
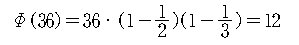 ? ?
|