선형 Diophantine 방정식
주어진 정수 a, b, n 에 대하여 이원일차방정식
ax + by = n
을 만족하는 정수 x, y 를 구하는 문제는 여러 가지 풀이
방법을 생각할 수 있다. 본 강의에서는 앞에서 학습한
세기의 방법을 활용하여 구하도록 한다.
일반적으로 위와 같이 정수계수의 대수방정식의 정수해를
구하는 문제를 부정방정식 또는 Diophantine 방정식
이라고 한다. 이에 관하여는 정수론책을 참고하기
바랍니다.
풀이. 방정식이 해를 순서쌍 (x,y,z) 라고 표시하면, 구하는 해는
(4, 1, 1), (3, 2, 1), (3, 1, 2), (2, 3, 1), (2, 2, 2),
(2, 1, 3), (1, 4, 1), (1, 3, 2), (1, 2, 3), (1, 1, 4)
의 모두 10개가 있다. ?
봅시다.
먼저 6 을 다음과 같이 표현하면
1 + 1 + 1 + 1 + 1 + 1 = 6
이제 양의 정수해 ( x , y , z ) 를 구하기 위하여는 위의 표현에서
2개의 +부호를 선택하면 된다. 즉,
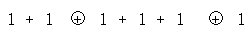
와 같이 골랐다면,
( x , y , z ) = (2 , 3 , 1 )
로 생각할 수 있다. 따라서 구하는 해의 개수는

개 이다. ?
정리 1. 자연수 m 에 대하여
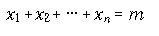
에서 모든 xi 가 양의 정수인 해의 개수는
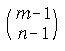
개이다.
|
증명.앞의 방법에서와 같이 ( m - 1 ) 개의 + 부호 중에서 ( n - 1 )
개의 + 부호를 고르는 방법의 수이다. ?
예제 2. x + y + z + w = 15를 만족하는 양의 정수해
(x,y,z,w) 의 개수는 모두 몇 개인가?
|
풀이.
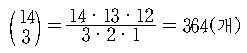
?
문제 1. x + y + z + w = 13을 만족하는 양의 정수해
(x,y,z,w) 의 개수는 모두 몇 개인가?
|
앞의 예제 1에서 조건을 약간 바꾸어 생각한다.
예를 들어, 방정식 에서 음이 아닌 정수해 의 개수를 구하여 봅시다.
그러면 5 개의 1 과 2 개의 +부호를 나열하여 구할 수 있다. 즉,
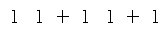
은
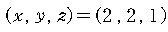
로 생각하고,
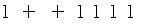
은
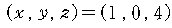
로 생각할 수 있다.
즉, 두 개의 +로 를 구별할 수 있으므로, 가능한 방법의 수는 5 개의 1 과
2 개의 +부호를 나열하는 방법의 수
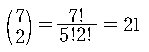
개이다.
따라서 다음의 정리를 얻을 수 있다.
증명. m 개의 1 과 ( n - 1 ) 개의 + 부호를 나열하는 방법의
개수이므로
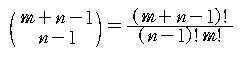
?
예제 3. x + y + z + w = 15를 만족하는 음이 아닌
정수해 (x,y,z,w) 의 개수는 모두 몇 개인가?
|
풀이. 구하는 해의 개수는
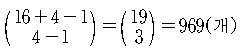
?
x + y + z = 16 의 정수해 중에서 x, y, z 가
모두 2 보다 큰 경우의 정수해의 개수를 구하여 봅시다.
먼저 방정식의 미지수를 바꾸어
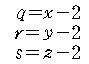
라고 두면, q , r , s 는 모두 양의 정수가 된다. 그러면
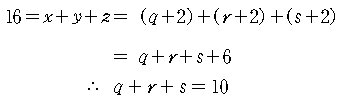
따라서 x + y + z = 16 이고 x, y, z 가 모두 2 보다 큰
정수해를 구하는 문제는 q + r + s = 10 이고 q , r , s 가
모두 0보다 큰 정수 ( 자연수 ) 해 를 구하는 문제로 바뀌었다. 따라서
정리 1 에 의하여 구하는 해의 개수는
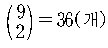
이다.
풀이. 주어진 방정식의 미지수를 다음과 같이 바꾼다.
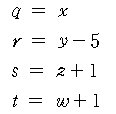
그러면, q, r, s, t 모두 자연수가 된다.
이 들을 원 방정식에 대입하여 정리하면
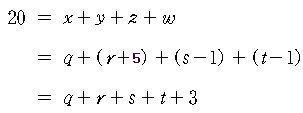
따라서 q + r + s +t = 17 을 만족하는 자연수해 의 개수를
구하는 문제이므로, 정리 1에 의하여
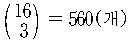
?
|