이항확률 (binomial probabilities)
예제 1. ○, ×로 답하는 문제가 6개 있다. 학생이 아무
생각도 없이 ○, ×표를 할 때, 적어도 2 문제가 맞을
확률을 구하여라.
|
풀이 . 각 문제에 대하여 맞을 확률은 1/2 , 틀릴 확률은 1/2 이다.
적어도 2 문제가 맞을 경우는 5 문제 이상이 틀리는 것의 여사건이므로
우선 6 문제 모두 틀릴 경우와 6 문제 중 5문제가 틀릴 경우의 확률을
구하여 계산한다.
먼저 6 문제 모두 틀릴 경우의 확률 :
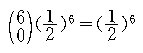
6 문제 중 5 문제가 틀릴 경우의 확률 :
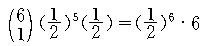
따라서 5 문제 이상 틀릴 경우의 수는
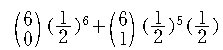
이고, 구하는 확률 P 는
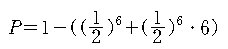
이다. ?
예제 2. 영희는 4명의 애들이 있는 가정에서 보모를 하고
있다. 이 때 아이들이 모두 남자일 확률은 얼마인가?
또, 2명이 남자, 2명이 여자일 확률은 얼마인가?
(단, 임의의 아이가 남자일 확률은 0.49, 여자일 확률은
0.51 이라고 가정한다. )
|
풀이.
(1) 4 명 모두 남자일 확률은
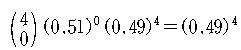
(2) 2 명이 남자, 2 명이 여자일 확률은
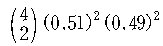
즉, 남자를 B, 여자를 G라고 하면 4명의 아이가
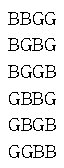
의 6 가지 경우가 있으며, 각각의 경우는 (0.51)2 (0.49)2이다.
?
위의 두 예에서 볼 수 있듯이, 모든 시행에서
(ⅰ) 항상 2가지 경우만 나타난다.
(예를 들면, ○, × ; 남자, 여자 ; 성공, 실패)
(ⅱ) 확률은 모든 시행에 있어 꼭 같다.
(ⅲ) 모든 시행은 독립적이다.
인 성질을 갖는 시행을 Bernoulli trials (베르누이 시행)
이라고 한다.
여자를 success (S)
남자를 failure (F)
라고 두고, S 일 확률은 p, F 일 확률은 q 라 하면,
q = 1 - p
또, 모든 시행은 S 와 F 중의 하나이고 , 독립적이다.
이때, k 개의 S 와 (n-k) 개의 F 가 있을 확률은
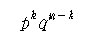
이다. 또, 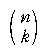 가지의 방법이 가능하므로 구하는 확률은 가지의 방법이 가능하므로 구하는 확률은
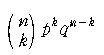
이다.
정리 3. n 개의 Bernoulli 시행에서, 성공일 확률이
p 일 때, k 개가 성립할 확률은
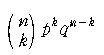
이다. 여기서 q = 1 - p 이다.
|
예제 3. 6명의 남자에 대하여 생명보험정책을 결정하려고
한다. 이 때 각 사람이 앞으로 20년 더 생존할 확률을
0.60 이라고 가정하자. 이 때,
(1) 4명이 앞으로는 20년 더 생존할 확률은 얼마인가
(2) 적어도 4명이 20년 더 생존할 확률은 얼마인가?
|
풀이.
(1) n = 6 , k = 4 이고
p = 0.60 , q = 1- p = 0.40 이므로 구하는 확률은
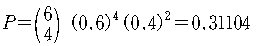
(2) 적어도 4명이 20년간 더 생존할 확률은
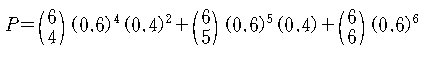
?
예제 4. A 마을의 유권자 중에서 공화당 지지가 62%,
민주당 지지가 38%이다. 이 때, 5명의 유권자를 임의로
골랐을 때, 정확히 한 명이 민주당 지지자일 확률은
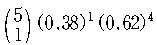
또, 5명의 유권자를 임의로 골랐을 때, 적어도 한 명
이상이 민주당 지지자일 확률은
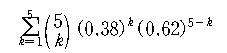
또는, 여사건으로 계산하면,
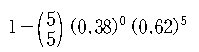
|
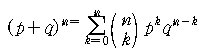
그런데 p + q = 1 이므로, 모든 사건의 확률의 합은 1 임이
분명하다. 즉,
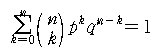
Ei 는 모든 가능한 사건을 나타내고, p(Ei) , P(Ei) 를 각각 사건 Ei
가 일어날 확률과 상금이라고 가정하면 이 시행의 기대값 E는
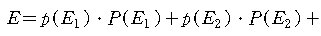
임을 이미 증명하였다.
베르누이 시행에서 보상금을 성공한 시행 회수만큼 준다고
가정하면, 이 때 기대값 E를 알아보도록 합시다.
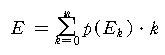
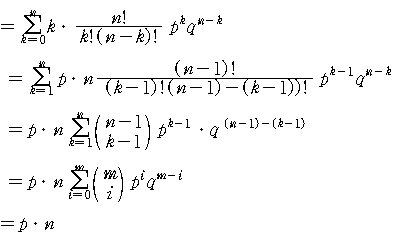
따라서 성공 확률이 p 인 베르누이 시행을 n 번 시행하였을 때 성공할
시행의 기대값은 pn 이다.
(이항분포에서의 평균은 np , 분산 npq 임을 확인하세요. )
예제 5. 방송퀴즈에서 엽서로 응모할 때 당첨되면 음악회
입장권을 준다. 이 때, 당첨될 확률은 25%이다.
(1) 이 때, 4통의 엽서를 응모하여 기대되는 음악회의
입장권의 기대값은?
(2) 또, 6장 엽서를 응모하여서 적어도 한 장 이상의
입장권을 얻을 확률은?
|
풀이.
(1) k 장의 입장권을 얻을 수 있는 확률은
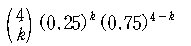
이므로, 입장권의 기대값 E 는
E = 4 * 0.25 = 1
(2) 여사건을 이용하면,
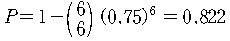
문제 1. 동전을 9번 던졌을 때, 앞면이 정확히 5번 나올
확률은 얼마인가 구하시오.
|
문제 2. 주사위를 세 번 던졌을 경우, 다음 각 사건의
확률을 구하시오.
⑴ 2가 한 번도 나오지 않을 경우
⑵ 2가 한 번 나올 경우
⑶ 2가 두 번 나올 경우
⑷ 2가 세 번 나올 경우
⑸ ⑴부터 ⑷까지의 확률의 합은?
|
문제 3. 3 문제 중 2 문제를 풀 수 있는 학생이, 4 문제
중에서 2 문제를 풀면 합격되는 시험에서 합격할 확률을
구하여라.
|
|