제 3장   이항정리와 그 응용

                

                  1.  이항정리  

   1.  이항정리

 

 

( x + y )10  의 전개식에서   x6 y4의  계수를

    구하시오.

 

     

     앞에서 학습한 counting technique을 더욱 발전시켜서

     다양한 세기의 방법으로 이항정리를 증명하고 그 응용을

     알아보도록 한다.

     

 

 

 

 

 이항정리 (Binomial Theorem)

  

이제 앞에서 학습한 counting technique 을 더욱 발전시켜서

다양한  세기( counting)의 방법을 알아보도록 합시다.

 

    먼저   다음 정리를 시작합시다.

 

     

    정리 1.  이항 정리 (Binomial Theorem)

    n이 자연수일 때,

                 (1)

     

 

증명. 자연수에 관하여 기술된 명제는 수학적 귀납법 (induction)으로 증명

하는 것이 일반적이다.

먼저 n=1일 때는

                               =  우변

    n=2 일 때,

    n=k 일 때 준식이 성립한다고 가정하라.  즉

   그러면,  n=k+1 일 때,

    따라서 수학적 귀납법에 의하여 모든 자연수 n에 대하여 위 식이

성립한다.    ?

 

 

    위의  연역적 증명방법과는 달리 다음과 같이 직관적으로

    구하여 봅시다.

(1+x)n = (1+x) (1+x) ... (1+x)

이고, 각 항은 1과 x 중 한 가지를 선택하여  n 번을 거듭하여 곱하여

구하여야 한다.  xr 의 계수는 x 를 r 번 고르는 조합수  

이고 1은 나머지 (n - r)개를 고르게 된다. 따라서 xr의 계수는

이고,

을 얻을 수 있다.

 

    위의 이항으로된 전개식에서  xr 의 계수

을 이항계수 (binomial coefficient)라고 부른다.

 

우리는 이항정리로부터  다양한 항등식을 얻을 수 있다.  

 

 

    예제 1.   식 (1)에서 x=1을 대입하면

 

 

 

 

     

    예제 2. 식 (1)에서 x = -1을 대입하면

 

 

 

    예제 2 로부터 우리는 다음을 얻을 수 있다.

 

 

     

    예제 3. 식 (1)의 양변을 각각 적분하면

     

    그런데 x = 0을 대입하면

    따라서

 

     여기에서 x = 1 을 대입하면

따라서

 

 

 

 

     

    문제 1. 다음 이항계수의 식의 값을 구하시오.

    (1)

    (2)

    (3)

    (4)

 

 

 

 

이항정리의 식 (1) 을 양변을 각각 미분하면

 

위 식에서 x =-1 을 대입하면,

또  x = 1 을 대입하면,

식 (a)와 (b)를 더하면,  n 이 짝수일 때,

n이 홀수일 때,

  

    이상에서 볼 수 있듯이 이항정리에서부터 많은

항등식을 우리는 증명할 수 있다. 이와 같은 이항계수의

항등식을 다음 표에서 참고하기 바란다.

 

 The top ten binomial coefficient identities

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

     

    정리 2.  n이 자연수 일 때,

 

 

증명.

?

 

 

 

     

    예제 4. ( 3x + y )12 의 전개식에서  x10 y2 의 계수를

    구하시오.

     

 

풀이. 정리2 에 의하여 x10y2의 계수는

 

    

이므로 ,      310  x  66                  ?

 

 

 

     

    문제 3. 다음 식을 전개할 때 주어진 항의 계수를

    구하여라.

        (1)   (a + b)4 에서 ab3 의 계수

        (2)   (x2 + x)7에서 x9 의 계수

         

 

 

 

      

    앞에서 학습한 counting technique을 더욱 발전시켜서

    다양한 세기의 방법으로 이항정리를 증명하고 그 응용을

    알아보았다. 

     

 

 

 

 

 

 

 

 

 

 

 

 

 

  제 3장   이항정리와 그 응용

                

       2.  다양한 이항 항등식 (Binomial Identities)

 

 

   2.  다양한 이항 항등식

 

     

    x 에 관한 다항식   ( 1 + 2x )4  ( 1 - x )5  의

    전개식에서  x2 의 계수는 얼마인가 구하시오. 

     

     

    본 강좌에서는 이항정리로 부터 유도되는 여러 가지

    유용한 이항 항등식을 알아 보고 그 응용을 학습한다.

     

 

 

 

 

              다양한 이항 항등식

 

    앞에서 살펴 본 이항항등식은 여러 가지 다양한 이항

항등식의 시작에 불과하다.  이제 좀 더 정교한 이항항등식을

살펴 보도록 합시다.

 

 

     

    예제 1. 다음 이항계수의 식을 증명하시오.

 

 

 

증명.   좌변은 이항정리의 적분의 형태이다 .

이항정리로부터 식을 변형하여

 

 

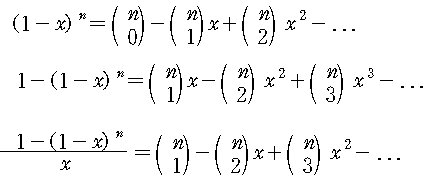
양변을  0에서 1까지 정적분하면,

 

 

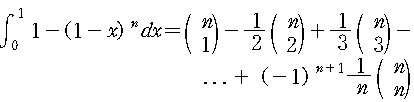
그런데 좌변의 정적분은 y = 1 - x 의 치환을 통하여

 

 

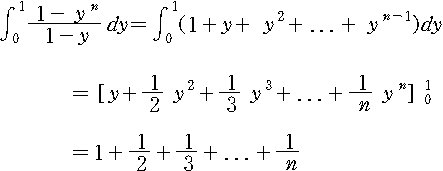
따라서 위 이항 항등식이 증명되었다.    ?

 

 

    위의 증명에서 볼 수 있듯이  식의 변형은 여러 가지 문제

해결에 결정적인 도움을 준다.

 

   예를 들면, 명제

 "모든 유리수는 서로 다른 분모를 갖는 조화수열의 합으로 표시

할 수 있다."

를  다음과 같은  탐구적 사고로 해결 할 수 있다.

 

모든 자연수 n에 대하여

 

 

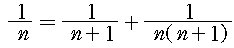
이므로  임의의 유리수

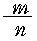
에 대하여

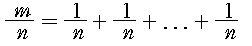
이고,

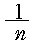
은

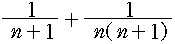
로 표시할 수 있으므로 모든 유리수는 서로 다른 분모를 갖는 조화수열의

합으로 표시할 수 있다.  예를 들면 ,

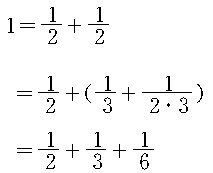
과 같이 표시할 수 있다.

 

 

    이항정리로부터 얻을 수 있는 항등식 중에서 다음의 식은

간단하면서도 매우 중요하다.

 

 

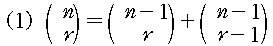
첫 번째 증명 :

 

 

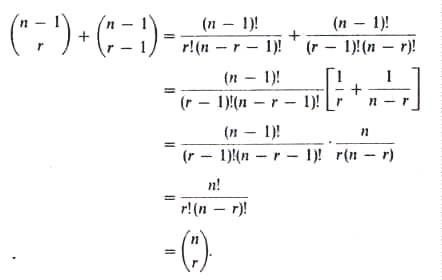
두 번째 증명 :

 

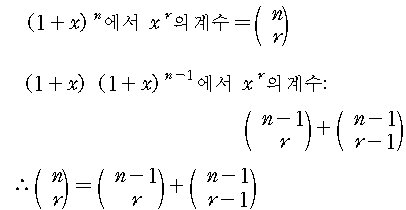
세 번째 증명 : n개 의 대상에서 r개 를 고르는 방법은

 

여기에서 어떤 특정한 대상 A를 정하고 , A가 포함되면서 r-1개를

고르는 경우와 A가 포함되지 않으면서 r개를 고르는 경우를 각각

생각하면

 

   ?

 

    위 식 (1)을 일반화 하면 다음과 같다.

 

 

  

 

     

 

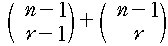
식 (1)은  Pascal의 삼각형으로도 불리며, 다음 그림에서의 삼각형 모양과 같다.

 

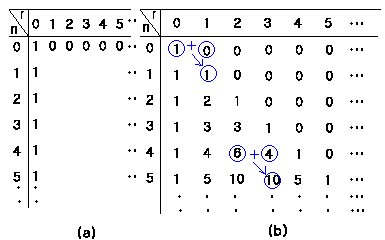
    이제 다음 이항계수의 항등식을 증명하여 봅시다.

 

   

         모든 자연수 n에 대하여 다음이 성립한다.

   (2)           

 

 

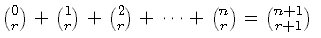
증명. 먼저

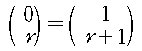
은 자명하다.

수학적 귀납법의 원리에 의하여

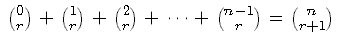
이 성립한다고 가정하라. 그러면

 

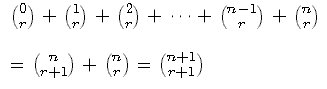
따라서 식 (2) 는  모든 자연수 n 에 대하여 성립한다.

모든

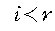
에 대하여 실제로

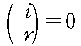
이므로 식 (2)는

 

 

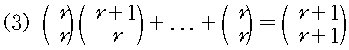
와 같이 표현 할 수 있다.

식 (3) 에서 특별히

 

 

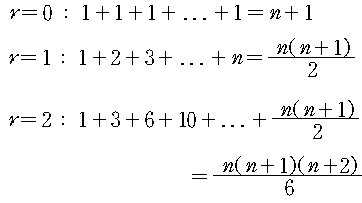
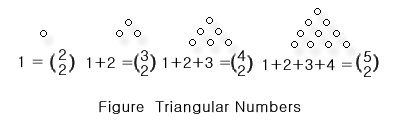
r =1인 경우에 식 (3)은 다음 그림에서와 같이 삼각수 ( triangular

numbers ) 가 된다.

또, r=2 인 경우에 식 (3) 은 입체적인 피라미드수 ( pyramidial

numbers ) 가 된다.


 

 

     

    문제 3.  평면 위의 어떤 3개도 동일한 점에서

    만나지 않는 8개의 직선이 있다.  8개 중 2개만이

    평행할 때, 이 들 8개의 직선으로 만들어지는

    교점의 개수와 삼각형의 개수를 각각 구하시오.

     

 

 

    이항계수

      

은  다음 그림과  같은 도로지도에서 유용한 응용을 얻는다.

 

 

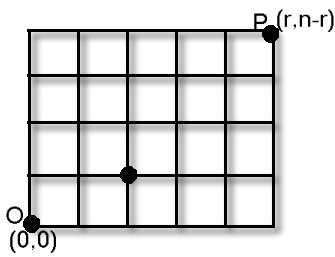
    원점 O에서 출발하여 점 P(n, r)까지 가는 최단의 경로의

경우의 수를 구하여 보자.

O에서 P까지의 최단거리는 반드시 n-r개의 세로 (A)와 r개의 가로

(B)를 지나야 하고 A와 B는 적당히 나열할 수 있으므로 모두

 

 

가지의 방법이 있다. 예를 들면, P(2,1)인 경우 가능한 최단 경로의

경우는

ABB, BAB, BBA

의 세 가지 경우이고

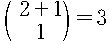
이다.

 

 

     

    문제 4. 원점 O 에서 출발하여 점 P(4,6)까지

    가는최단 경로의 경우의 수를 구하여라

     

   

 

     

     본 강좌에서는 이항정리로 부터 유도되는 여러 가지

    유용한 이항항등식을 알아 보고 그 응용을 학습하였다.