조건부 확률과 기대값
오랜 시간을 두고 예상 되는 평균의 의미를 갖는다고 말할 수
있다.
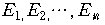
이 생길 수 있고, 각각의 사건
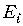
가 일어날 확률을
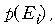
각각의 사건
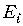
에 대한 보상 (상금 또는 벌금 등)을
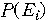
라하면, 이 게임을 할 때 기대할 수 있는 기대금액 E 는
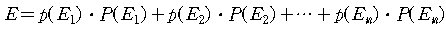
으로 약속한다. 이같은 값 E를 우리는 이
게임의 기대값 (expectation of the game ) 이라고 한다.
예제 1. 10,000 명이 어떤 TV 경품대회에 우편엽서로
응모를 하였다.
이 때, TV 경품대회의 당첨자는 1 명이고, 상품으로는
20 만원 상당의 TV를 준다고 하면, 각자 기대할 수 있는
기대값은 얼마인가 알아보시오. (단, 우편엽서의 값은
200원이라고 하자.)
|
풀이. 각자 당첨될 확률은
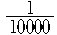
이고, 상금은 200,000 원, 또 각자 당첨안될 확률은
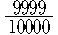
이고, 비용은 200원 이므로, 기대값 E는
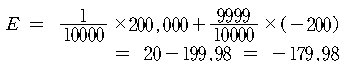
따라서, 기대값이 음수이므로 각자에게 손해가 예상되는 게임이라고 할 수
있다. ?
다음은 The Gane of Mastermind 라고 불리는 게임이다.
예제 2. 각각 다른 색이 칠하여진 막대 7 개 중에서 6
개를 골라서 6 개의 hole에 각각 한 개씩 꽂았다. 이 때,
막대를 모두 꺼낸 후 다시 막대 7 개 중에서 6 개의
막대를 임의로 골라서 다시 hole에 꽂을 때, 처음의
경우와 같은 색이 들어 있을 hole의 기대 개수는
얼마인가 알아보시오.
|
풀이. i = 0, ..., 6 에 대하여 사건
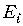
를 각각 ( 6 - i ) 개가 일치하는 사건이라고 하면, 각각의 i 에
대하여
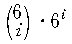
개의 경우가 가능하다. ( 이것은 i 개가 틀리게match되는 경우의 수를 의미
한다.) 그러면 나머지 (6-i)개는 일치하므로 (즉, 한 가지이므로) 색이 일치
하는 hole의 개수의 기대값 E 는
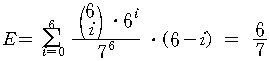
또 이 문제의 해결은 다음과 같이 간단한 추측 방법도 있다.
한 개의 hole에 관심을 두면, 처음의 경우와 같은 색으로 일치될 확률은
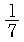
이고, 일치되지 않을 확률은
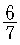
이다. 따라서 기대값은
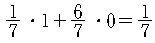
그런데 모두 6 개의 hole이 있으므로 전체로 기대할 수 있는 hole 의
기대값은
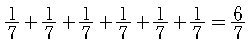
이다. ?
위의 풀이를 보면, 어떤 의미에서는 확률보다 기대값이 더 좋은
현실적인 의미를 갖는다고 해석할 수 있다.
문제 1. 갑과 을 두 사람이 있다. 갑은 6개의 동전을 갖고
있고,을은 5개의 동전을 갖고 있다.
이 때, 두 사람이 동전을 모두 던졌을 때, 갑이 던진
동전의 앞면의 수가 을이 던진 동전의 앞면의 수보다 더
많을 확률을 구하시오.
|
문제 2. (The St. Petersburg Paradox) 두 사람 A,
B가 동전을 던져 앞면이 나오면 이기는 게임을 한다.
이 때, n 번째 toss에서 앞면이 나오면A가 B에게 2n
만원을 주기로 한다.
그러면 B는 A에게 얼마를 지불하여야 이 게임이 공정한
가를 생각하여 보시오.
(실제로
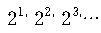
이 지불되는 사건이 일어날 확률은각각
2-1, 2-2, 2-3…
이므로, B가 기대할 수 있는 수입은 무한하다고 볼 수
있다. 즉,
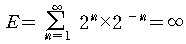
따라서, 이것은 B가 A에게 무한대의 금액(?)을 지불
하여야 이 게임이 공정하다는 의미인가를 생각하여
보시오.)
|
이제 조건부확률에 대하여 알아보도록 합시다.
한 대학의 신입생 n명 중에서 남자가nB 명, 여자가(n-nB)명 있고,
신입생 중에서 안경을 쓴 사람은 nA명 있다고 하자.
이 대학의 신입생 중에서 한 명을 임의로 택할 때, 안경을 쓴 사람이 뽑힐
사건을 A, 남자가 뽑힐 사건을 B 라 하면 이 실험에서 A와 B의 확률은
각각
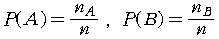 (1) (1)
로 주어진다.
또한, 신입생 중에서 남자이며 안경을 쓴 사람의 숫자를
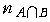
로 나타내면, 이와 같은 실험에서 남자이며, 안경을 쓴 사람이 뽑힐 사건
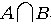
이 일어날 확률은
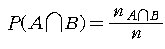 (2) (2)
로 주어진다.
이제 신입생 중의 일부인 남자 신입생 중에서 한 명을 랜덤하게 택하는
경우를 생각해 보자.
이 때에는 안경을 쓴 사람이 뽑힐 사건 A의 "확률"은
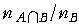
임은 명백하다.
즉, 이 경우에는 실험 결과 전체의 집합이 B로 국한됨으로써 사건 A의
"확률" 이 식 (1)과 달리 주어진다. 따라서, 이 경우에는 실험 결과 전체의
집합이 B임 을 확실히 하기 위하여 사건 A의 "확률"을
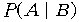
라는 새로운 기호로 나타내고, 이를 "사건 B가 주어진 경우에 사건
A의 확률"이라 부른다. 즉, 이와 같이 B를 전제로 하는 실험에서 사건 A의
확률은 다음과 같이 주어진다.
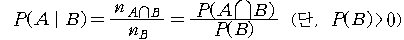 (3) (3)
로 정의한다.
이상에서 알아본 바와 같이, 주어진 표본공간 S의 일부인
한 사건 B를 전제로 하는조건부 실험을 생각할 수 있다.
이 때 생각할 수 있는 확률의 개념은 일반적인 경우와 같으며,
단지 사건 B를 전제로 하는 점이 다를 뿐이다.
일반적으로, 사건 B가 주어진 경우, 사건 A의
조건부 확률 (conditional probability)을
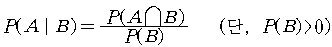
로 정의한다.
새로운 표본공간으로 축소시킨 실험에서의 확률을 뜻한다.특히, 원래의
실험이 등확률 모형인 경우에는 식 (3) 과 같이 조건부 확률을 계산할 수
있다.
예제 3. 검은 공이 b 개, 흰 공이 w개, 빨간 공이 r개 들어
있는 상자에서 k 개의 공을 동시에 추출한다고 하자.
이제, 꺼내어진 k개의 공 중에서 j 개가 빨간 공인 것을 알
때, 나머지 k-j 개 중에서 i 개가 흰 공일 확률을 구하여
보시오.
|
풀이. 동시추출된 k개의 공 중에서 j개가 빨간 공일 사건을 B, i개가 흰
공일 사건을 A라고 하자. 사건 B가 주어진 경우에는 동시추출된 k 개중에서
j 개의 빨간 공을 제외한 (k-j)개의 공을 b개의 검은 공과 w개의 흰 공이
들어 있는 상자에서 동시 추출 하는 것으로 생각할 수 있다. 따라서, 구하는
확률은
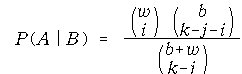
로 주어진다. 실제로, 정의에 의해 조건부 확률 P(A|B) 를 구하여 보면
이와 같은 값을 얻을 수 있다.
다음의 예는 조건부 확률을 생각할 때 원래의 실험의 기술, 즉
표본공간의 표현에 유의해야 하는 경우를 보여준다.
예제 4. 동전 두 개를 던지고 그 결과를 직접 관측하지 못하고,
두 동전 중에서 하나가 앞면임을 알았을 때, 다른 하나의
동전도 앞면으로 나타났을 조건부 확률을 구하여 보자.
|
동전의 앞면과 뒷면을 각각 H,T로 나타내면 이 경우에
표본공간
Ω = {HH, HT, TH, TT}
로 나타낼 수 있고, 각 경우의 확률은 1/4로 주어진다. 그리고
두 동전 중에서 하나가 앞면으로 나타나는 사건은
A = { HH, HT, TH }
로 주어지고, 두 동전 모두가 앞면으로 나타나는 사건은
B = { HH }
로 주어진다. 따라서, 구하는 조건부 확률은
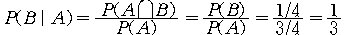
로 주어진다.
다음에는, 동전 두 개를 던지고 그 결과를 모두 관측하지
못하고 두 동전 중에서 하나만을 볼 수 있다고 하자. 이 때,
관측된 동전이 앞면으로 나타났을 때 다른 하나의 동전도
앞면일 확률을 구하여 보자.
이 경우에는 어느 동전이 선택되어 관측 되는 것인지를 명확히
하여 표본공간을 생각할 필요가 있다.
관측되는 동전이 첫 번째인 경우와 두 번째인 경우를 각각 1,2
로 나타내면, 표본공간을
(*)
Ω= {HH1, HH2, HT1, HT2, TH1, TH2, TT1, TT2}
로 나타낼 수 있다. 여기에서 HT1은 동전이 나타난
결과는 HT 이고 관측된 것은 첫 번째 동전임을
나타낸다. 물론, 여기에서 각 경우의 확률은 1/8로
주어진다.
식 (*)와 같이 표본공간을 나타내면, 관측된 동전이
앞면일 사건은
C = {HH1, HH2, HT1, TH2}
이고 두 동전이 모두 앞면으로 나타날 사건은
D = {HH1, HH2}
로 주어진다. 따라서, 구하는 조건부 확률은
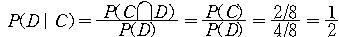
로 주어짐을 알 수 있다. ?
조건부 확률의 응용
일반적으로, 확률에 관한 문제에서는 여러 개의 사건들을
다루게 되고 이들 상호간의 관계를 파악하는 것은 확률의
계산에서 필연적인 과정이다. 이러한 과정에서 조건부 확률은
매우 유용하게 쓰일 수 있다.
이제부터 조건부 확률의 기본적 성질을 살펴보고 이의 이용의
예를 알아보기로 한다.
첫째로, 조건부 확률의 정의로부터
P(A∩B) = P(A|B). P(B) ( P(B)>0 )
임은 명백하다. 이를 n개의 사건에 축차적으로 적용시키면
P(A1∩A2)=P(A2|A1)P(A1) ( P(A1)>0 )
P(A1∩A2∩A3)=P(A3|A1∩A2)P(A1∩A2)
(P(A1∩A2)>0 )
…………
P(A1∩...∩An)
= P(An|A1∩...∩An-1)P(A1∩...∩An-1)
임을 알 수 있다. 따라서, 다음의 정리를 얻을 수있다.
정리 A. 임의의 사건 A1,...,An 에 대하여
P(A1∩...∩An-1)>0 이면,
P(A1∩...∩An)=P(A1)P(A2|A1)P(A3|A1∩A2)
...P(An|A1∩...∩An-1)
|
사건의 독립성
일반적으로 사건 B가 주어진 경우에 사건 A의 조건부
확률 (A|B)는 A의 확률 P(A)와 같지 않다. 즉, 사건
B의 출현 여부에 관한 정보는 사건 A의 출현
가능성에 변화를 주는 것이다.
그런데, 특수한 경우로서 P(A|B) = P(A) 이면 B의
출현 여부에 관한 지식은 사건 A의 출현
가능성에 아무런 영향을 미치지 않는다는 뜻이다. 이러한
의미에서 P(A|B) = P(A) , 즉
P(A∩B) = P(A) P(B) (**)
일 때, 사건 A와 B는
서로 독립(mutuallyindependent)이라 한다. 식
(**)에서는 P(B) = 0 인 경우도 포함되어 있으며,
사건 A와 B는 대칭적인 역할을 하고 있음에 유의할
필요가 있다.
예제 5. 흰 색과 빨간 색의 주사위 두 개를 던질 때,
흰 색 주사위의 눈이 홀수일 사건을 A, 빨간 색
주사위의 눈이 짝수일 사건을 B, 두 주사위의 눈의
합이 홀수일 사건을 C라 하자. 이 때, 표본공간의
경우의 수는 36 이고, 사건 A의 경우의 수는 3 x 6 =
18 , 사건 B의 경우의 수는 6 x 3 = 18 , 사건 C의
경우의 수는 2 x 2 x 3 = 18 이므로,
P(A)P(B)P(C) = 18/36 = 1/2
이다. 또한 , A∩B = B∩C = C∩A 이고 A∩B 의
경우의 수는 3 x 3 = 9 이므로,
P(A∩B) = P(B∩C) = P(C∩A) = 9/36 = 1/4
이다. 따라서,
P(A∩B) = P(A)P(B)
P(B∩C) = P(B)P(C)
P(C∩A)= P(C)P(A)
가 성립하므로, A와 B, B와 C, C와 A는 서로
독립이다. ?
|
이제 두 사건의 독립성의 개념을 세 사건의 경우로
일반화하는 것에 대하여 생각해 보자. 예제 5 에서와
같이
P(A∩B) = P(A)P(B)
P(B∩C) = P(B)P(C)
P(C∩A)= P(C)P(A)
가 성립하면, 세 사건 A, B, C 중에서 임의의 두
사건이 독립임을 뜻하므로 세 사건 A, B, C는 쌍으로
독립(pairwise independent) 이라 한다. 한편, 예제
5에서 A ∩B ⊂ C 이므로,
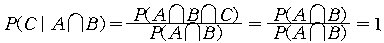
이고, 이는 P(C) = 1/2 과 같지 않음을 알 수 있다.
즉, A, B, C는 쌍으로 독립이지만, A와 B의 출현
여부에 관한 지식이 중첩되면 C의 출현 가능성에
영향이 미치는 것이다. 그러므로, 이러한 경우에는 세
사건 A, B, C가 진정한 의미로 "독립"이라고 할 수는
없는 것이다. 따라서, 이러한 경우를 배제하기 위하여
세 사건 A, B, C에 대하여
P(A∩B) = P(A)P(B)
P(B∩C) = P(B)P(C)
P(C∩A)= P(C)P(A)
P(A∩B∩C) = P(A)P(B)P(C) (3)
이 성립할 때, 세 사건 A, B, C는 서로 독립(mutually
independent)이라 한다.
예제 5에서는
P(A∩B∩C) = P(A∩B) ≠ P(A)P(B)P(C)
이므로, 세 사건 A, B, C 는 쌍으로 독립이지만 서로
독립은 아니다. 서로 독립인 세 사건에 대하여는 예제
5와 같은 경우가 일어나지 않음은 다음 정리로부터 알
수 있다.
정리 B.
⒜ A, B, C가 서로 독립이면 A, B도 서로 독립이다.
⒝ A, B, C가 서로 독립이면 A도 서로 독립이다.
⒞ A, B, C가 서로 독립이면 A도 서로 독립이다.
|
증명 .A∩B∩Cc = A∩B - A∩B∩C 이고
A∩B∩C⊂A∩B 이므로,
P(A∩B∩Cc) = P(A∩B) - P(A∩B∩C)
이다. 따라서, A, B, C가 서로 독립이면 식 (3)으로부터
P(A∩B∩Cc) = P(A∩B) - P(A∩B∩C)
P(A)P(B) - P(A)P(B)P(C)
P(A)P(B)P(Cc)
이다. 같은 방법으로,
P(Bc∩C) = P(Bc)P(C) , P(C∩Ac)= P(C)P(Ac)
P(A∩B) = P(A)P(B)
이 성립함을 보일 수 있다. 그러므로 ⒜가 성립한다.
한편
P(A∩(B∪C)) = P((A∩B)∪(A∩C))
가 성립하므로, A, B, C가 서로 독립하면 식(3)으로부터
P(A∩(B∪C)) = P(A∩B) + P(A∩C)
P(A∩B∩C)=P(A)P(B)+ P(A)P(C)-P(A)P(B)P(C)
= P(A)P(B) + P(C) - P(B∩C)
= P(A)P(B∪C)
가 성립한다. 즉, ⒝가 성립한다. 마지막으로, A, B, C가 서로
독립이면 식 (3)으로부터
P(A∩(B∩C)) = P(A∩B∩C)
= P(A)P(A)P(C) = P(A)P(B∩C)
임을 알 수 있게 되어, ⒞가 성립한다. ?
정리 B1 로부터, 세 사건 A, B, C가 서로 독립이면 이들 중에서
임의의 두 사건으로 표현될 수 있는 사건은 나머지 한 사건과
서로 독립임을 알 수 있다.
일반적으로, n개의 사건 A1, A2, ... ,An이 있는 경우에는 임의의
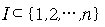 에 대하여 에 대하여
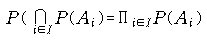
가 성립하면 사건이 서로 독립(mutually independent)이라
한다. 즉 임의의 1 ≤ I < j < k < ... ≤ n 에 대하여
P(AI∩Aj) = P(AI)P(Aj)
P(AI∩Aj∩Ak) = P(AI)P(Aj)P(Ak)
……………
P(AI∩Aj∩ ... ∩An) = P(AI)P(Aj)P...(An)
이 성립할 때, 사건이 서로 독립이라 한다. 이와 같이 n개의
사건의 독립성을 정의하면 정리 B와 같은 방법으로 다음이
성립함을 보일 수 있다.
정리 C.

|
|