두 가지 세기(Counting)의 방법
문제. 원형의 탁자에 5쌍의 부부가 앉으려고 한다.
이 때,남자와 여자는 교대로 앉아야 하고, 부부는 옆에
나란히 앉을 수 없다고 한다. 그러면 앉을 수 있는 방법
은 모두 몇 가지나 되는지 알아보시오.
|
일상 생활 중에서 우리는 위의 문제와 같은 많은 상황을
만나게 되며, 우리는 이와 같은 문제를 해결하기 위하여 여러
방법의 세기(counting)를 잘 하여야 한다.
(1) 순서(order)를 고려하던지 또는 고려하지 않던지;
(2) 반복(repetition)을 허락하던지 또는 허락하지 않던지
등을 고려하여 여러 조건 하에서 선택이나 분포를 counting
하는 것은 중요한 문제이며 , 지금부터 차례대로 알아보기로
합시다.
예제 1. 개인사물함에 두 자로 된 명찰을 붙여서 구분
하려고 한다. 한글 `가, 나, 다, ... , 파, 하 ` 의 14자
중에서 한 글자와 수자 `0, 1, 2, ... , 8, 9`의 열 개중
한 수자를 사용하려고 한다. 이 때 사물함을 구별할 수
있는 명찰을 몇 개 만들 수 있는지 알아보시오.
|
풀이. 사물함의 명찰의 모양은
한글 : 수자 (예를 들면, 가 3 )
수자 : 한글 (예를 들면, 4 라 )
의 경우가 가능하므로,
한글 : 수자 의 경우는 14 x 10 = 140 (가지)
수자 : 한글 의 경우는 10 x 14 = 140 (가지)
따라서, 구별할 수 있는 사물함의 명찰의 개수는 모두
140 + 140 = 280 (개)
이다. ?
위 예제 1에서 알 수 있듯이, k 개의 가능성이 있는 일이
독립적으로 시행될 수 있고, 또 각각의 경우의 수가
m1, m2, ..., mk 일 때, 가능한 전체의 경우의 수는 모두
이다. 이것을 합의 법칙 (the addition principle)이라고 한다.
각각의 경우의 수가 m1, m2, ..., mi 인 연속된 일을 시행할 때,
가능한 전체의 경우의 수는 모두
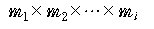
이다. 이것을 곱의 법칙 (the multiplication principle)이라고
한다.
이 두 가지 법칙은 모든 경우의 세기 문제에 있어서 가장 기본적인
법칙이다.
예제 2. 15명의 회원을 가진 어떤 모임이 있다. 이 때,
회장, 부회장, 총무, 감사를 각각 선출하려고 한다.
가능한 경우의 수는 모두 몇 가지인가 ?
|
풀이. 회장, 부회장, 총무, 감사를 연속하여 선출하여야 하므로, 곱의
법칙에 의하여
15 x 14 x 13 x 12 (가지) ?
예제3. 빨간 주사위 R과 파란 주사위 B를 동시에 던질
때 나올 수 있는 눈의 경우의 수를 구하여 보시오.
또, 동일한 두 주사위를 던질 때 나올 수 있는 눈의
경우의 수도 구하여 보시오.
|
풀이.
(1) 빨간 주사위 R의 눈이 나올 수 있는 경우의 수는 6 가지
파란 주사위 B의 눈이 나올 수 있는 경우의 수는 6 가지
따라서 곱의 법칙에 의하여 구하는 경우의 수는 모두
6 x 6 = 36 (가지)
이를 구체적으로 구하여 보면, 빨간 주사위 R과 파란 주사위 B의 나온 각각
눈을 r, b 라 하고 순서쌍 (r, b)로 표시하면
(1,1), (1,2), (1,3), (1,4), (1,5), (1,6)
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6)
...
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)
(2) 동일한 두 주사위를 던지는 경우에 위의 경우에서의 (1,2)와 (2,1)은
구별할 수가 없고, 같은 모양으로 이해되므로 가능한 전체의 경우의 수는
모두
1 + 2 + 3 + 4 + 5 + 6 = 21 (가지) ?
위 예제는 우리가 곧 학습할 중복순열과 중복조합의 전형적인 예로서,
경우 (1)은 중복순열
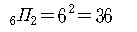
이고, 경우 (2)는 중복조합
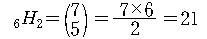
이다.
문제 1. 세 자리의 양의 정수 중에서 7, 8, 9 를
자리수에 모두 갖고 있지 않은 정수는 몇 개인가
알아보시오.
|
순서가 있는 선택의 문제 (Ordered choices)
m 개의 대상으로부터 r 개를 선택할 경우에,
(1) 중복을 허락하는가?
(2) 순서를 고려하는가?
를 고려하여 경우의 수를 계산하여야 한다.
S가 공집합이 아닌 집합일 때, 중복을 허용하고 순서를 고려하여
r 개를 선택한 부분집합을 S의 r 표본(r-sample)이라 한다.
S의 원소의 개수를 n이라 하고, r표본의 개수를 구하여
봅시다.
먼저 순서를 고려하므로 r개의 방을 먼저 순서대로 나열하고
□ □ □ … □
각 방에는 S의 원소 n 개 중에서 임의로 한 개를 선택할 수 있으므로
곱의 법칙에 의하여
n×n×…×n= nr
이며, 이것을 중복순열이라고 부른다
정리1. S의 원소의 개수를 n이라 하면, r 표본의
개수는
n×n×…×n= nr 이다.
|
예제 1. 운동복에 0부터 9까지의 수자를 사용하여 두
자리 수자를 붙이려 한다. 그러면 중복순열의 수이므로,
102= 100 가지의 운동복 번호를 붙일 수 있다.
즉, 00 부터 99 까지 모두 100 가지이다.
|
문제 2. 26자의 영어 알파벳 중에서 5자 사용하여 임의로
낱말 모양을 만들려고 한다. 가능한 낱말은 모두 몇 가지
인가?
|
이것을 binary code 라고 한다. 0,1 중 한 개로 이루어진 정보를 1 bit
라 하고 8 bit를 1byte라고 한다. 이때, 1byte code의 가능한 경우의
수를 살펴보면 중복순열의 원리의 의하여
2 x2 x···x 2 =26 = 64 (가지)
가 가능하다.
개인용 PC는 정보처리 단위에 따라서 8 bit, 16 bit , 32 bit , 64 bit
등과 같이 한 번에 처리할 수 있는 정보양으로 PC를 구분하여 부르며,
요즘 Pentium Ⅱ processor를 갖춘 PC를 64 bit 운영체제인 PC라고
부른다.
이 때, 4 byte (32bit) code의 경우의 수를 알아보면 중복순열의 수에
의한 경우의 수는 모두
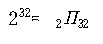
이다. 이 숫자는 앞에서 학습한 Hanoi Tower 문제에서 나온 숫자에
버금가는 커다란 수이다.
문제 3. 2 byte 조합형 한글의 경우, 한글의
최소정보량은 2 byte이다. 이 때, 2 byte 조합형
한글code의 가능한 모든 경우의 수를 구하시오.
|
문제 4. 아이스크림의 향의 종류가 10가지 이고 ,
아이스크림 컵에 두 주걱의 아이스크림을 담을 경우,
가능한 아이스크림 종류의 경우의 수를 모두 구하여라.
또 , 두 주걱의 아이스크림이 서로 다른 경우 가능한
아이스크림 종류의 경우의 수를 모두 구하여라.
|
보도록 합시다.
집합 S의 r-sample 중에서 원소가 모두 다른 것들을 우리는
r-순열 (r- permutation) 이라고 부른다. 또, S의 원소의
개수가 r 인 경우에 S의 r-순열은 단순히 순열 (permutation)
이라고 한다.
정리 2. S의 원소의 개수가 n 일 때, r-순열의 수는
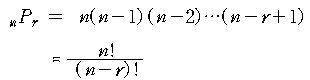
이다. |
증명. r-순열은 모두 다른 원소를 r 개 골라서 순서대로 나열하는 방법의
수이므로, 곱의 법칙을 사용하면
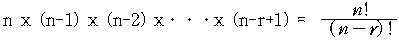
이다. ?
기호의 약속
(1) n = r 일 때 : 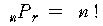
(2) r = 0 일 때 : 0-순열은 의미가 없다. 그러나 계산의 편의를
위하여 모든 n에 대하여
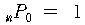
로 약속한다.
실제로 n ! 은 Gamma 함수로 정의되는 수의 특수한 경우로
이해되는 수로서, p > 0 인 임의의 실수 일 때 함수는 다음과 같이
정의된다 :
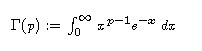
그러면 모든 p > 0 에 대하여 점화식
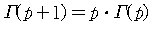
가 성립하고, 이 때 특별히 p가 자연수이면
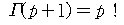
가 된다. ( 공학수학이나 해석학 책을 참조하시오.)
|
예제 4. 12명의 회원을 가진 모임에서 서로 다른 직함을
갖는 4 명을 선출하는 방법의 경우의 수는 ?
|
풀이.
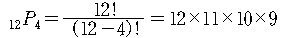 ? ?
예제 5. 알파벳 A, B, C, D 가 각각 쓰여진 네 장의
카드를 모두 사용하여 만들 수 있는 단어는 모두 몇
가지인가 알아보시오.
|
풀이.
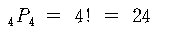 ? ?
|