격자다각형(lattice polygon)의 문제
지난 강좌의 하노이탑 문제에 이어서 마지막으로
이산수학에서 전형적인 예를 알아봅시다.
점들로 구성된 격자평면 (lattice plane)을 생각하여 봅시다.

이 때, 아래의 그림에서와 같이 원점 O에서 주위를 바라
보았을 때, 곧바로 보이는 점 (예를 들면, 점 P와 같은 점)을
visible point 라고 하고, 다른 점에 가로 막혀서 보이지 않는
점 (예를 들면, 점 Q와 같은 점)을 invisible point라고 한다.
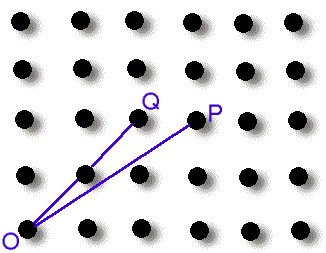
그러면 어떤 점이 visible point이고, 어떤 점이 invisible
point인가를 결정하는 문제를 알아보도록 합시다.
먼저 invisible point Q(m,n)은 원점 O와 점 Q를 잇는 선분 OQ
위에 분명히 가로 막는 격자점 Q'(m',n')이 있다. 따라서, 점 Q의 x, y
좌표 m, n 은 각각 점 Q'의 좌표 m', n'의 배수임이 분명하다. 즉, m 과
n의 최대공약수 d는 1 보다 큰 수이며, 서로 소가 아님이 분명하다.
반면에, visible point P(m,n)인 경우에는 중간에 가로 막힌 점이
없으므로 ,점 P 의 x , y 좌표 m, n은 어떤 격자점의 좌표의 배수가
되어서는 안된다. 따라서, m 과 n의 최대공약수 d는 1 이며, 두 수 m, n
은 서로 소 이다.
예제 1. 점 P(17, 23)과 Q(26,46)은 각각 visible
point 인가를 결정하시오.
|
풀이. 점 P의 최대공약수 gcd( 17 , 23 ) = 1 이므로, 점 P는
visible point 이다. 또,
점 Q의 최대공약수 gcd ( 26 , 46 ) = 2 이므로,
점 Q 는 invisible point이다. 즉, 점 Q'( 13 , 23 )이
점 Q를 가로 막고 있다. ?
이제 위의 문제를 일반화하여 두 점 P(m, n), Q(r, s)가
서로 바라 볼 수 있는가를 결정하여 봅시다.
우리는 위 문제에서 평행이동을 사용하면 앞의 문제로 바꾸어 생각할 수
있다. 즉, 점 P를 원점 O로 평행이동하면, 점 Q는 Q'(r - m, s - n)
으로 평행 이동이 됨을 알 수 있다. 따라서, 우리는 두 수 r - m, s - n 이
서로 소인가 아닌가를 판정하면 충분하다. 이 때, 서로 바라볼 수 있는
점들을 mutually visible points(서로 바라볼 수 있는 점들)
라고 부른다. 즉, 다음 그림에서 두 점 P와 Q는 mutually visible
points이다.
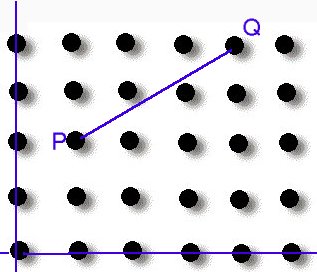
예제 2. 점 P(26, 13)과 Q(5, 5)는 서로 바라볼 수 있는
가를 결정하시오.
|
풀이. 점 Q를 원점으로 평행이동하면, 점 P는 새로운 점
P'(26 - 5, 13 - 5) = (16, 8)
이 된다. 따라서, x, y 좌표의 최대공약수d = (16, 8) = 8 이므로 서로
바라볼 수 없다. 즉, 중간에 어떤 다른 격자점이 놓여 있다. ?
문제 1.
(1)점 P(17,23 ) 과 Q( 5 , 7 )은 서로 바라볼 수
있는가를 결정하시오.
(2) 점 P(14, 26 ) 과 Q( 6 , 8 )은 서로 바라볼 수
있는가를 결정하시오.
|
문제 2. 격자평면 위에서 원점 O를 지나는 직선
y = 3x
를 그리고, 직선 위에 있는 격자점들의 x, y 좌표들의
관계를 알아보시오.
|
직선은 기울기에 따라서 여러 가지 모양으로 변할 수 있다.
이 때, 원점 이외의 어떤 격자점도 지나지 않는 직선이 존재할
수 있는가를 생각하여 봅시다.
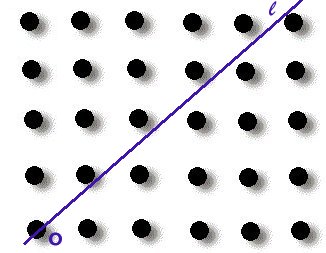
우리는 이 문제의 해결의 실마리를 어디부터 찾아야할까요 ?
몇 번의 걸쳐서 직선을 그려보고 해결의 열쇠를 구하도록 합시다.
우선 우리가 관찰한 바에 의하면, 직선에서 가장 중요한 data는 기울기임을
알 수 있다. 만약 직선 이 원점 이외의 격자점 P(m,n)을 지난다면,
직선의 기울기는 유리수
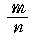
이다. 따라서
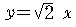
와 같이 무리수 기울기를 갖는 직선은 원점 이외의 격자점을 지날 수 없다.
이와 같은 사고방법을 귀류법적 사고방법이라고 하며, 많은 (수학)문제들이
귀류법을 사용하여 해결될 수 있다.
(연역법과 반대인 증명법)을 사용하는 증명이다.
앞에서와 같이 위 문제는 보다 높은 차원 ( 3차원, 4차원 등 ) 으로
일반화 할 수 있다. 이에 대하여 각자 연구하여 보시오.
봅시다.
|
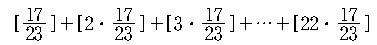
단, [x] 는 x를 넘지 않는 최대의 정수 (Gaussian
Integer Function)를 나타낸다.
|
풀이.
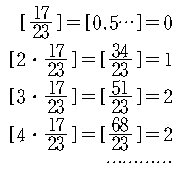
추측하기 어렵다.
이제 주어진 식을 관찰하여 보면, 다음 그림에서 볼 수 있듯이
격자평면 위의 직선
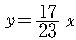
와 밀접한 관계가 있음을 알 수 있다. 즉, 우리의 문제는 x 축 위에
있으며 직선 아래에 있는 격자점의 개수를 구하는 문제로 바꾸어 생각할 수
있다. 따라서 가장 중요한 요소는 직선
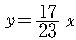
위에 과연 격자점이 있는가의 확인이다. 그런데 기울기
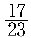
에서 17 과23은 서로 소이므로 직선 위에는 어떤 격자점도 없음을 알 수
있다. ( 왜냐하면, 만약 어떤 격자점이 있다면 17 과 23 은 각각 그 좌표의
배수이므로 서로 소가 될 수 없다 ! )
따라서 우리가 구하는 격자점의 개수는 전체 직사각형 안의 격자점의
개수의 반에 해당하므로,
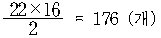
이다. ?
문제 6. a와 b가 서로 소인 자연수일 때, 다음을 간단히
계산하시오.
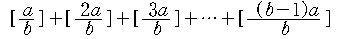
단, [x] 는 x를 넘지 않는 최대의 정수 (Gaussian
Integer Function)를 나타낸다.
|
이와 같이 문제해결 (problem solving)를 할 때, 그림을
사용하여 문제해결의 실마리를 풀어가는 것은 대표적인
탐구방법 (heuristic method ) 이다.
생각하여 봅시다.
문제 7 .격자평면 위에서 한 점을 임의로 택할 때, 그
점이 visible point (즉, 원점 O 에서 보이는 점)일
확률은 어느 정도가 되는지 알아보시오.
|
풀이. 이 문제는 앞에서 생각한 문제와 같이 기울기에 관한 사고를 통하여
해결할 수 있다. 즉, 임의로 고른 한 점을 P(m,n)이라고 하면, 두 수 m,
n이 서로 소가 되어야 P점이 visible point가 된다. 따라서, 위 문제는
자연수 에서 두 수 m과 n을 임의로 선택할 때 서로 소가 될 확률을 구하는
문제가 된다. 이 것은 약간 복잡한 계산이 필요하지만 다음과 같이 그 풀이를
소개 한다 :
Let g be the greatest common divisor of
two integers a and b,that is g = (a,b) and let p be the
probability* that g = 1. We will first show that the probability
that g = n for n = 1,2,... is p/n2 .
Clearly the probability that n divides both a and b is 1/n2 .
The probability that no proper multitple of n divides both a
and b is the same as the probability that (a/n, b/n) = 1,
which is p. Thus, the probability that g = n is p/n2 .
The sum of the probabilityes that g = n for n = 1, 2,
... must equal 1, so that
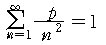
Solving for p, we obtain
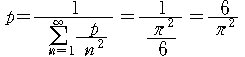
*The probability is defined by
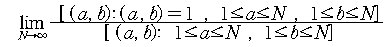
?
문제 8. 격자평면 위에서 두 점을 임의로 택할 때, 그
점이 서로 보일 (mutually visible points) 확률은
얼마인가 알아 보시오.
|
위에서 학습한 바와 같이 많은 그림이나 도형에 관한 수학문제들은
대수적 또는 기하적인 여러 방법에 의하여 해결할 수 있는 방법이
있음을 알 수 있다.
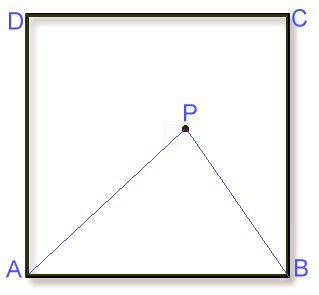
문제 9. 정사각형 ABCD 안에 임의의 한 점 P를 택하여
만들어진 삼각형 ABP가 예각삼각형이 될 확률은
얼마인가 알아보시오.
|
|