Conditions
This is an in-class test to be completed from 6:00 pm to 9:00 pm on Tuesday, 7 May.

Please write each solution in the blank or in the space provided under each prob lem situation. Use additional sheets of paper only as necessary. In evaluating your work, I need to be able to determine how you have solved each problem as well as any assumptions you have made. Leave a mathematical trail for me to follow.

You may not share work with others but you may use other resources (notes, textbook, worked exercises, and so on). You may use a calculator. You may express solutions in factorial notation or other combinatorial symbolism.

Impact on Grade
The semester exam accounts for 20% of your course grade.

Evaluation Criteria
You may earn up to 15 points for each problem. For each solution:

€ 12 points count toward a correct solution to the problem: Here I will consider the mathematics you use. Is it accurate and appropriate? Have you provided justification for your work?

€ 3 points count toward how you express your solution: Here I will consider how you communicate your solution. Is it clear and complete? Is it well organized?


Part I: Questions for Small-Group Exploration


1. While lounging in the lobby of the Embassy Suites hotel in San Diego, I watched hotel employees open a door after entering a code by pushing a digital keypad. The keypad is similar to the one shown here.

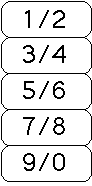
From my vantage point, I could see neither the door nor the keypad. I could see people pushing buttons from the side. After carefully watching several people enter the door, I concluded that the sequence of keystrokes they used looked like the figure shown below.


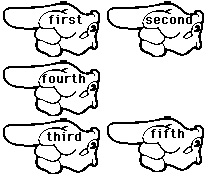
€ I knew the order of the keystrokes, as indicated by "first, second" and so on shown here.

€ I did not know which keypad was struck first.

€ I did know that the fourth push was directly below the first and second, and that the third and fifth pushes were directly below the fourth.







Based on this information, determine the number of different 5-number codes that could possibly unlock this door.

2. Forty-one (41) pennies are placed on a 10-by-10 grid, one in each square of the grid. Prove that for any such placement, it is possible to choose a set of five pennies so that no two are in either the same row or the same column.
3. A certain zookeeper has n cages in a row and two indistinguishable lions. The lions must be in separate cages, and they may not be placed in adjacent cages. Determine the number of ways that the zookeeper can assign the 2 lions to the n cages.
4. In the May 1996 issue of the Mathematics Teacher (p 368), R. S. Tiberio of Wellesley (MA) High School shared the following student discovery:


Your task: Justify that this relationship will hold in general, or, alternatively, show that the result cannot be generalized to all of Pascal's triangle.


Part II: Questions for Individual Exploration

1. Consider the letters in the word purchase.

a. How many unique arrangements exist for the letters in the word?
b. If an arrangement must begin with a consonant and end with a vowel, how many unique arrangements exist for the letters in the word?

2. At Bagwanna State University, students' programs of study must include course credit in mathematics, science, English, history, and the arts. Each student must complete a total of exactly 46 credits that include these areas of study. Furthermore, no less than 6 credits must be in mathematics, at least 8 credits must be in science, and 10 or more credits must be from English. How many different student programs, based on credits earned, can be designed under these restrictions?
3. Consider the expansion of (R + D + A + Y)^16.

a. Determine the number of uncollected terms in the expansion.
b. Determine the number of collected terms in the expansion.
c. Determine the coefficient P of the collected term PD^6A^2Y^8.
d. How many collected terms in the expansion will have the numerical coefficient P that you determined in (c) above?

4. A shelf is to contain nine different books, six different paperback books and three different hardback books. If the paperback books must be shelved in pairs (that is, exactly two paperback books must be adjacent to each other), how many ways can the nine books be shelved?